题目内容
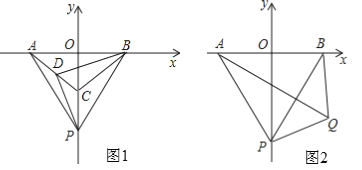
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.

(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
【答案】(1)(a+b)2,a2+b2+2ab; (2)(a+b)2=a2+2ab+b2;(3)①ab=7 ;② (2018﹣a)(a﹣2017)=﹣2.
【解析】
(1)两个小正方形的面积加上矩形的面积即可得出大正方形的面积或者直接运用大正方形的边长求解即可;
(2)由面积关系容易得出结论;
(3)①根据(2)所得出的关系式,容易求出结果;
②先根据题意得出(2018﹣a)与(a﹣2017)的等量关系,即可得出结果.
(1)(a+b)2,a2+b2+2ab;
(2)(a+b)2=a2+2ab+b2;
(3)① ∵a+b=5,
∴(a+b)2=25,
∴a2+b2+2ab=25,
又∵a2+b2=11,
∴ab=7 ;
② 设2018﹣a=x,a﹣2017=y,则x+y=1,
∵(2018﹣a)2+(a﹣2017)2=5,
∴ x2+y2=5,
∵(x+y)2=x2+2xy+y2,
∴xy=![]() =﹣2,
=﹣2,
即(2018﹣a)(a﹣2017)=﹣2.

【题目】某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 安全知识测试成绩频数分布表
组别 | 成绩x(分数) | 组中值 | 频数(人数) |
1 | 90≤x<100 | 95 | 10 |
2 | 80≤x<90 | 85 | 25 |
3 | 70≤x<80 | 75 | 12 |
4 | 60≤x<70 | 65 | 3 |

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为人.