题目内容
已知:m是非负数,抛物线y=x2-2(m+1)x-(m+3)的顶点Q在直线y=-2x-2上,且和x轴交于点A、B(点A在点B的左侧).
(1)求A、B、Q三点的坐标.
(2)如果点P的坐标为(1,1).求证:PA和直线y=-2x-2垂直.
(3)点M(x,1)在抛物线上,判断∠AMB和∠BAQ的大小关系,并说明理由.
(1)求A、B、Q三点的坐标.
(2)如果点P的坐标为(1,1).求证:PA和直线y=-2x-2垂直.
(3)点M(x,1)在抛物线上,判断∠AMB和∠BAQ的大小关系,并说明理由.
(1)设抛物线的顶点Q的坐标是(x,y),
则x=-
=m+1,y=
=-m2-3m-4;
∵点Q(m+1,-m2-3m-4)在直线y=-2x-2上,
∴-m2-3m-4=-2(m+1)-2,
解得m1=0,m2=-1;
∵m是非负数,舍去m2=-1,
∴m=0;
∵抛物线解析式为y=x2-2x-3,令y=0,
∴得x2-2x-3=0,
解得x1=-1,x2=3,
∴A(-1,0),B(3,0),Q(1,-4);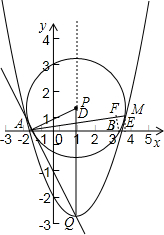
(2)如图,∵抛物线的对称轴是直线x=1,
∴P点在对称轴上,
∴PQ=|1-(-4)|=5;
把A(-1,0)代入y=-2x-2,-2x(-1)-2=0成立,
∴A点在直线y=-2x-2上;
设PQ交x轴于点D,则PQ⊥AB;
在Rt△ADQ中,AQ2=AD2+QD2=20,
在Rt△APD中,AP2=AD2+PD2=5,
∴AQ2+AP2=20+5=25=PQ2;
∴△PAQ是直角三角形,∠PAQ=90°;
∴PA⊥AQ,
∴PA和直线y=-2x-2垂直;
(3)答:∠AMB=∠BAQ;
解法一:
M(x,1)在抛物线y=x2-2x-3上,
∴1=x2-2x-3,
解得x=1±
,
∴点M的坐标为(1+
,1),PM=|1+
-1|=
,
∴PA=PM=PB=
;
于是点A、M、B都在以点P为圆心,
为半径的圆上,如图,
∵AQ⊥AP,
∴AQ是⊙P的切线,
∴∠BAQ=∠AMB;
当x=1-
时,点M的坐标为(1-
,1);
同理可得∠BAQ=∠AMB.(15分)
解法二;当x=1+
时,作ME⊥x轴于点E,如图,则点E的坐标为(1+
,0);
于是ME=1,EA=1+
+1=2+
,
AM=
=
=
,
连接BM,作BF⊥AM于F,AB=|3-(-1)|=4,
则S△ABM=
ME•AB=
AM•BF
∴1×4=
•BF
∴BF=
在△MBE中,∠MEB=90°,
BM=
=
=
在△BFM中,∠BFM=90°,
sin∠BMF=
=
=
=
在△DAQ中,∠ADQ=90°,
∵sin∠DAQ=
=
,
∴sin∠BMF=sin∠DAQ
而∠BMF、∠DAQ都是锐角,
∴∠BMF=∠DAQ,即∠AMB=∠BAQ;
当x=1-
时,同解法一.
则x=-
| -2(m+1) |
| 2 |
| -4(m+3)-[-2(m+1)]2 |
| 4 |
∵点Q(m+1,-m2-3m-4)在直线y=-2x-2上,
∴-m2-3m-4=-2(m+1)-2,
解得m1=0,m2=-1;
∵m是非负数,舍去m2=-1,
∴m=0;
∵抛物线解析式为y=x2-2x-3,令y=0,
∴得x2-2x-3=0,
解得x1=-1,x2=3,
∴A(-1,0),B(3,0),Q(1,-4);

(2)如图,∵抛物线的对称轴是直线x=1,
∴P点在对称轴上,
∴PQ=|1-(-4)|=5;
把A(-1,0)代入y=-2x-2,-2x(-1)-2=0成立,
∴A点在直线y=-2x-2上;
设PQ交x轴于点D,则PQ⊥AB;
在Rt△ADQ中,AQ2=AD2+QD2=20,
在Rt△APD中,AP2=AD2+PD2=5,
∴AQ2+AP2=20+5=25=PQ2;
∴△PAQ是直角三角形,∠PAQ=90°;
∴PA⊥AQ,
∴PA和直线y=-2x-2垂直;
(3)答:∠AMB=∠BAQ;
解法一:
M(x,1)在抛物线y=x2-2x-3上,
∴1=x2-2x-3,
解得x=1±
| 5 |
∴点M的坐标为(1+
| 5 |
| 5 |
| 5 |
∴PA=PM=PB=
| 5 |
于是点A、M、B都在以点P为圆心,
| 5 |
∵AQ⊥AP,
∴AQ是⊙P的切线,
∴∠BAQ=∠AMB;
当x=1-
| 5 |
| 5 |
同理可得∠BAQ=∠AMB.(15分)
解法二;当x=1+
| 5 |
| 5 |
于是ME=1,EA=1+
| 5 |
| 5 |
AM=
| ME2+EA2 |
12+(2+
|
10+4
|
连接BM,作BF⊥AM于F,AB=|3-(-1)|=4,
则S△ABM=
| 1 |
| 2 |
| 1 |
| 2 |
∴1×4=
10+4
|
∴BF=
| 4 | ||||
|
在△MBE中,∠MEB=90°,
BM=
| BE2+ME2 |
(1+
|
10-4
|
在△BFM中,∠BFM=90°,
sin∠BMF=
| BF |
| BM |
| ||||||
|
| 4 | ||||||||
|
| 2 | ||
|
在△DAQ中,∠ADQ=90°,
∵sin∠DAQ=
| DQ |
| AQ |
| 2 | ||
|
∴sin∠BMF=sin∠DAQ
而∠BMF、∠DAQ都是锐角,
∴∠BMF=∠DAQ,即∠AMB=∠BAQ;
当x=1-
| 5 |

练习册系列答案
相关题目
 平面直角坐标系.
平面直角坐标系.
 上部分点的横坐标与对应的纵坐标如下表:
上部分点的横坐标与对应的纵坐标如下表:

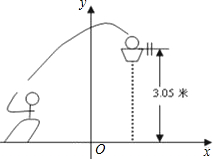 框内.已知篮框的中心离地面的距离为3.05米.
框内.已知篮框的中心离地面的距离为3.05米.