��Ŀ����
�ھ���ABCD�У�AB=2��AD=4����AB�Ĵ�ֱƽ����Ϊx�ᣬAB���ڵ�ֱ��Ϊy�ᣬ������ͼ��ʾ��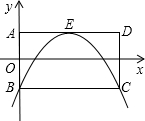 ƽ��ֱ������ϵ��
ƽ��ֱ������ϵ��
��1���������꣺A______��B______��C______��______��AD���е�E______��
��2������EΪ���㣬�Գ���ƽ����y�ᣬ���Ҿ�����B��C�������ߵĽ���ʽ��
��3����Խ���BD�����������߳���B�������һ����P�����ꣻ
��4����PEB�����S��PEB���PBC�����S��PBC���������Ĺ�ϵ��֤����Ľ��ۣ�
 ƽ��ֱ������ϵ��
ƽ��ֱ������ϵ����1���������꣺A______��B______��C______��______��AD���е�E______��
��2������EΪ���㣬�Գ���ƽ����y�ᣬ���Ҿ�����B��C�������ߵĽ���ʽ��
��3����Խ���BD�����������߳���B�������һ����P�����ꣻ
��4����PEB�����S��PEB���PBC�����S��PBC���������Ĺ�ϵ��֤����Ľ��ۣ�
��1��A��0��1����B��0��-1����C��4��-1����D��4��1����E��2��1����
��2���������ߵĽ���ʽΪy=a��x-2��2+1��
�������߾�����B��0��-1����
��a��0-2��2+1=-1�����a=-
��
�������ߵĽ���ʽΪy=-
��x-2��2+1��
����֤��������y=-
��x-2��2+1������C��4��-1����
��3��ֱ��BD�Ľ���ʽΪy=
x-1���ⷽ����õ�P�����꣺P��3��
����
��4��S��PEB=
S��PBC•S��PBC=
��4��
=3��S��PEB=
����1��2+1��1��=
��
��S��PEB=
S��PBC��
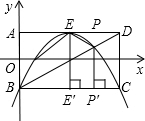
��2���������ߵĽ���ʽΪy=a��x-2��2+1��
�������߾�����B��0��-1����
��a��0-2��2+1=-1�����a=-
| 1 |
| 2 |
�������ߵĽ���ʽΪy=-
| 1 |
| 2 |
����֤��������y=-
| 1 |
| 2 |
��3��ֱ��BD�Ľ���ʽΪy=
| 1 |
| 2 |
| 1 |
| 2 |
��4��S��PEB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
��S��PEB=
| 1 |
| 2 |


��ϰ��ϵ�д�
�����Ŀ
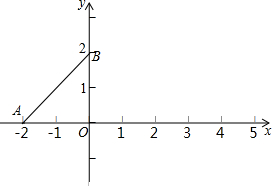 OC������A��ת����B��λ�ã���������y=ax2+bx+c��a��0������B��C���㣬��x�����һ������Ϊ��D������Ϊ��P���Գ���Ϊֱ��x=3��
OC������A��ת����B��λ�ã���������y=ax2+bx+c��a��0������B��C���㣬��x�����һ������Ϊ��D������Ϊ��P���Գ���Ϊֱ��x=3��

 ����������x��Χ�ɵ������
����������x��Χ�ɵ������
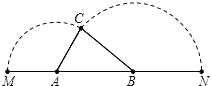 ��M����BΪ������ʱ����ת��N��ʹM��N�����غϳ�һ��C�����ɡ�ABC����AB=x��
��M����BΪ������ʱ����ת��N��ʹM��N�����غϳ�һ��C�����ɡ�ABC����AB=x��