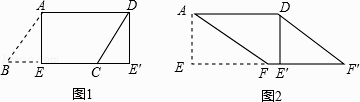��Ŀ����
����Ŀ���Ķ����в��ϣ�
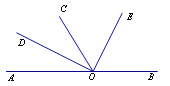
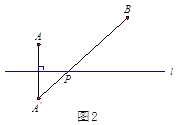
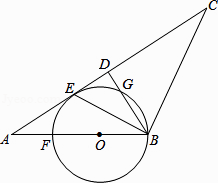
С������һ�����⣺AD�ǡ�ABC�����ߣ� ��MΪBC��������һ�㣨�����D�غϣ�������M��һֱ�ߣ�ʹ��ȷ֡�ABC�������
���������ǣ���ͼ1������AM������D��DN//AM��AC�ڵ�N����ֱ��MN��ֱ��MN��Ϊ����ֱ�ߣ�
����ο�С��������������������⣺
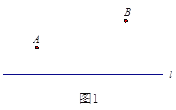
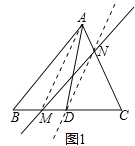
��1����ͼ2�� AE�ȷ��ı���ABCD�������MΪCD����һ�㣬��M��һֱ��MN��ʹ��ȷ��ı���ABCD�������Ҫ����ͼ2�л���ֱ��MN����������ͼ�ۼ�����
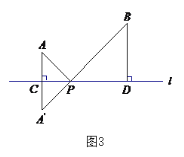
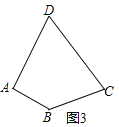
��2����ͼ3����������A��ֱ��AE��ʹ��ȷ��ı���ABCD�������Ҫ����ͼ3�л���ֱ��AE����������ͼ�ۼ�����

���𰸡�������
��������(1)������AM����E��EN��AM����AD��N������ֱ��MN���ɣ�(2)��ȡ�Խ���BD���е�O������AO��CO��AC������O��OE��AC��CD��E��ֱ��AE��������ֱ�ߣ�
��1����ͼ������AM����E��EN��AM����AD��N������ֱ��MN��
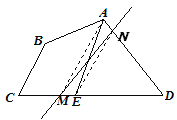
��2����ͼ��ȡ�Խ���BD���е�O������AO��CO��AC������O��OE��AC��CD��E��ֱ��AE��������ֱ�ߣ�


��ϰ��ϵ�д�
 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
�����Ŀ