题目内容
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
【答案】(1)购进甲种花卉每盆16元,乙种花卉每盆8元;(2)10≤x≤12.5,故有三种购买方案,在所有的购进方案中,购买甲种花卉12盆,乙种花卉76盆时,获利最大,最大利润是148元.
【解析】
(1)根据题意设购进甲种花卉每盆x元,乙种花卉每盆y元,列出相应的二元一次方程组,从而可以求得购进甲、乙两种花卉,每盆各需多少元;
(2)根据题意可以列出相应的不等式组,从而可以得到有几种购进方案,利用一次函数的性质得到哪种方案获利最大,最大利润是多少.
解:(1)设购进甲种花卉每盆x元,乙种花卉每盆y元,
![]() ,
,
解得:![]() ,
,
即购进甲种花卉每盆16元,乙种花卉每盆8元;
(2)设甲种花卉购进![]() 盆,则
盆,则
 ,
,
解得,10≤![]() ≤12.5,
≤12.5,
又![]() 为整数,
为整数,![]() =
=![]()
故有三种购买方案,
![]() 由利润W=
由利润W=![]()
![]() W随
W随![]() 的增大而增大,
的增大而增大,
故当![]() =12时,
=12时, ![]() ,
,
即购买甲种花卉12盆,乙种花卉76盆时,
获得最大利润,此时W=4×12+100=148,
即该花店共有几三种购进方案,
在所有的购进方案中,购买甲种花卉12盆,乙种花卉76盆时,获利最大,最大利润是148元.

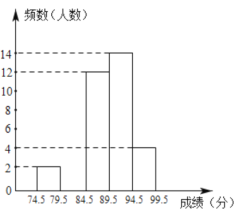
【题目】某校开展“祖国在我心中”主题演讲比赛,参加选拔比赛的选手的成绩(满分为![]() 分),分成五组,制成了如下不完整的统计图表.
分),分成五组,制成了如下不完整的统计图表.
分数段 | 频数 | 频率 |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
(1)求分数在![]() 参赛学生的频率;
参赛学生的频率;
(2)求分数在![]() 参赛学生的频数,并补全频数分布直方图;
参赛学生的频数,并补全频数分布直方图;
(3)成绩在![]() 分以上的选手中,有三名男生和一名女生,学校从中随机确定
分以上的选手中,有三名男生和一名女生,学校从中随机确定![]() 名选手参加市级比赛,求恰好是一名男生和一名女生的概率.
名选手参加市级比赛,求恰好是一名男生和一名女生的概率.
【题目】新冠肺炎疫情发生后,口罩市场出现热销,小明的爸爸用12000元购进医用外科、N95两种型号的口罩在自家药房销售,销售完后共获利2700元,进价和售价如下表:
品名价格 | 医用外科口罩 | N95口罩 |
进价(元/袋) | 20 | 30 |
售价(元/袋) | 25 | 36 |
(1)小明爸爸的药房购进医用外科、N95两种型号口罩各多少袋?
(2)该药房第二次以原价购进医用外科、N95两种型号口罩,购进医用外科口罩袋数不变,而购进N95口罩袋数是第一次的2倍,医用外科口罩按原售价出售,而效果更好的N95口罩打折让利销售,若两种型号的口罩全部售完,要使第二次销售活动获利不少于2460元,每袋N95口罩最多打几折?