��Ŀ����
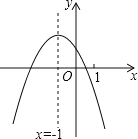
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=x+3�ֱ�x�ᡢy����A��C���㣬������y=ax2+bx+c��a��0��������A��C���㣬��x�ύ�ڵ�B��1��0����
��1���������ߵĽ���ʽ��
��2����DΪֱ��AC��һ�㣬��EΪ��������һ�㣬��D��E����ĺ����궼Ϊ2����FΪx���ϵĵ㣬���ı���ADEF��ƽ���ı��Σ���ֱ��д����F�����ꣻ
��3������P���߶�AC�ϵ�һ�����㣬����P��x��Ĵ��ߣ����������ڵ�Q������AQ��CQ������ACQ����������ֵ��
���𰸡���1��y=��x2��2x+3����2����7��0������3��![]() ��
��
��������
�����������1����x=0����ֱ�ߵĽ���ʽ��õ�C��0��3������y=0�������x=��3���Ӷ��õ���A����3��0�����������ߵĽ���ʽΪy=a��x+3����x��1��������C�������������a=��1���Ӷ��õ������ߵĽ���ʽΪy=��x2��2x+3��
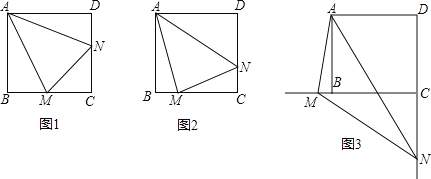
��2����x=2�ֱ����ֱ�ߺ������ߵĽ���ʽ����õ�D��2��5����E��2����5����Ȼ�����ƽ���ı��εĶԽ�����ƽ�ֿ���õ�F�����ꣻ
��3����ͼ2��ʾ�����P������Ϊ��a��a+3�������Q������Ϊ��a����a2��2a+3����QP=��a2��3a���������ε������ʽ��֪����ACQ�����=![]() ��
��![]() Ȼ�������䷽����ö��κ��������ֵ����
Ȼ�������䷽����ö��κ��������ֵ����
�⣺��1������x=0����y=x+3����y=3��
����C��������0��3����
����y=0����y=x+3�õ�x=��3��
����A����������3��0����
�������ߵĽ���ʽΪy=a��x+3����x��1��������C���������ã���3a=3��
��ã�a=��1��
�������ߵĽ���ʽΪy=����x+3����x��1����
�����ã�y=��x2��2x+3��
��2������x=2����y=x+3�ã�y=5��
����D��2��5����
��x=2����y=��x2��2x+3�ã�y=��5��
����E��������2����5����
��ͼ1��ʾ��
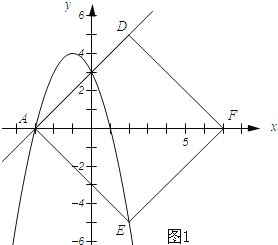
���ı���ADFEΪƽ���ı��Σ�
����F��������7��0����
��3����ͼ2��ʾ��
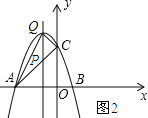
���P��������a��a+3�������Q��������a����a2��2a+3����
QP=��a2��2a+3����a+3��=��a2��2a+3��a��3=��a2��3a��
�ߡ�ACQ�����=![]() ��
��
���ACQ�����=![]() =
=![]() ��
��![]() =
=![]() ��a
��a![]() ��2+
��2+![]() ��
��
���ACQ����������ֵΪ![]() ��
��

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�