题目内容
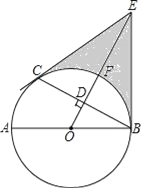
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
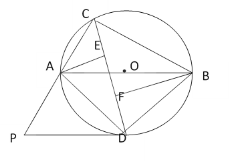
(1)求证:DP∥AB;
(2)试猜想线段AE、EF、BF之间的数量关系,并加以证明;
(3)若AC=6,BC=8,求线段PD的长.
【答案】(1)见解析;(2)BF-AE=EF,见解析;(3)![]()
【解析】
(1)由切线的性质可得∠ODP=90°,∠BOD=90°,从而根据“内错角相等,两直线平行”即可证明DP∥AB;
(2)先证明△ADE≌△DBF,得到BF=DE,AE=DF,进而根据线段的运算得到“BF-AE=EF”;
(3)由勾股定理运算得出AD,CE,CD的值,再根据PD∥AB得到∠PDA=∠ACD,从而证明△PAD∽△PDC,根据相似比计算得出PD即可.
解:(1)证明:连接OD,
∵PD切⊙O于点D,
∴OD⊥PD,∠ODP=90°
∵∠ACD=∠BCD,∠AOD=2∠ACD,∠BOD=2∠BCD,
∴∠AOD=∠BOD=![]() ×180°=90°,
×180°=90°,
∴∠ODP=∠BOD,
∴PD∥AB
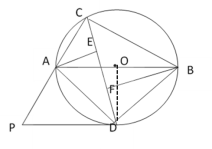
(2)BF-AE=EF,
证明如下:
∵AB是⊙O的直径
∴∠ADB=∠ADE+∠BDF=90°,
∵AE⊥CD,BF⊥CD
∴∠AED=∠BFD=90°,
∴∠FBD+∠BDF=90°,
∴∠FBD=∠ADE,
∵∠AOD=∠BOD
∴AD=BD
∴△ADE≌△DBF(AAS),
∴BF=DE,AE=DF
∴ BF-AE=DE-DF,
即BF-AE=EF
(3)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACD=![]() ∠ACB=45°,
∠ACB=45°,
在Rt△ACB中,AB2=AC2+BC2=100,
在Rt△ADB中,AB2=2AD2,
∴AD=5![]() ,
,
在Rt△AEC中,AC2=AE2+CE2,
∴AE=CE=3![]() ,
,
在Rt△AED中,DE=![]() =4
=4![]() ,
,
∴CD=CE+DE=7![]() ,
,
∵PD∥AB,
∴∠PDA=∠DAB,
∵∠ACD=∠BCD=∠DAB,
∴∠PDA=∠ACD,
又∵∠P=∠P,
∴△PAD∽△PDC,
∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
∴PA=![]() PD+6,
PD+6,
∴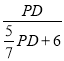 =
=![]() ,
,
∴PD=![]()

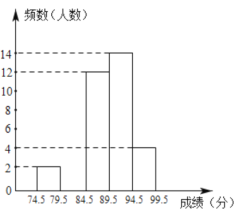
【题目】某校开展“祖国在我心中”主题演讲比赛,参加选拔比赛的选手的成绩(满分为![]() 分),分成五组,制成了如下不完整的统计图表.
分),分成五组,制成了如下不完整的统计图表.
分数段 | 频数 | 频率 |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
(1)求分数在![]() 参赛学生的频率;
参赛学生的频率;
(2)求分数在![]() 参赛学生的频数,并补全频数分布直方图;
参赛学生的频数,并补全频数分布直方图;
(3)成绩在![]() 分以上的选手中,有三名男生和一名女生,学校从中随机确定
分以上的选手中,有三名男生和一名女生,学校从中随机确定![]() 名选手参加市级比赛,求恰好是一名男生和一名女生的概率.
名选手参加市级比赛,求恰好是一名男生和一名女生的概率.