题目内容
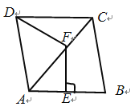
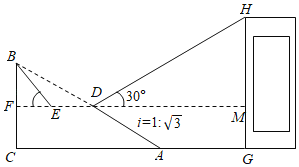
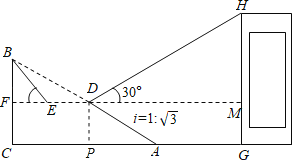
【题目】如图,育英学校前方有一斜坡AB长60米,坡度i=1:![]() ,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
(1)若修建的斜坡BE的坡角(即∠BEF)不大于45°,则平合DE最长是多少米?
(2)学校教学楼GH距离坡脚A点27米远(即AG=27米),小明在D点测得教学楼顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H在同一个平面上,点C、A、G在同一条直线上,且HG⊥CG,问:教学楼GH高为多少米?(结果精确到0.1米,参考数据![]() ≈1.732)
≈1.732)
【答案】(1)平合DE最长是11.0米;(2)教学楼GH高为45.6米.
【解析】
(1)由斜坡BE的坡角(即∠BEF)不大于45°,可得出当∠BEF=45°时,EF最短,此时ED最长,由斜坡AB的坡度可得出∠BAC=∠BDF=30°,由点D是AB的中点可得出AD,BD的长,通过解直角三角形可求出EF,DF的长,结合DE=DF-EF可求出平合DE最大值;
(2)过点D作DP⊥AC,垂足为点P,在Rt△DPA中,通过解直角三角形可求出PA的长,利用矩形的性质可求出DM的长,在Rt△DMH中,通过解直角三角形可求出HM的长,再结合GH=HM+MG可求出教学楼GH的值.
(1)∵斜坡BE的坡角(即∠BEF)不大于45°,
∴∠BEF最大为45°,
当∠BEF=45°时,EF最短,此时ED最长.
∵tan∠BAC=i=![]() ,
,
∴∠BAC=∠BDF=30°.
∵点D是AB的中点,
∴AD=BD=![]() AB=30米,
AB=30米,
∴BF=EF=![]() BD=15米,DF=15
BD=15米,DF=15 ![]() 米,
米,
∴DE=DF﹣EF=15(![]() ﹣1)≈11.0米.
﹣1)≈11.0米.
答:平合DE最长是11.0米.
(2)如图,过点D作DP⊥AC,垂足为点P.
在Rt△DPA中,DP=![]() AD=15米,PA=ADcos30°=15
AD=15米,PA=ADcos30°=15 ![]() 米.
米.
在矩形DPGM中,MG=DP=15米,DM=PG=PA+AD=(15 ![]() +27)米,
+27)米,
在Rt△DMH中,HM=DMtan30°=(15![]() +27)×
+27)×![]() =(15+9
=(15+9 ![]() )米,
)米,
∴GH=HM+MG=15+15+9![]() ≈45.6米.
≈45.6米.
答:教学楼GH高为45.6米.

【题目】某中学共有学生2000名,各年级男、女生人数如下表:
年级 | 六年级 | 七年级 | 八年级 | 九年级 |
男生 | 250 | z | 254 | 258 |
女生 | x | 244 | y | 252 |
若从全校学生中任意抽取一名,抽到六年级女生的概率是0.12;若将各年级的男、女学生人数制成扇形统计图,八年级女生对应扇形的圆心角为44.28°.
(1)求x,y,z的值;
(2)求各年级女生的平均数;
(3)如果从八年级随机抽取36名学生参加社会实践活动,求抽到八年级某同学的概率.