Question

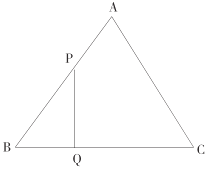
【题目】规定：经过三角形的一个顶点且将三角形的周长分成相等的两部分的直线叫做该角形的“等周线”，“等周线”被这个三角形截得的线段叫做该三角形的“等周径”．例如等腰三角形底边上的中线即为它的“等周径”Rt△ABC中，∠C＝90°，AC＝4，BC＝3，若直线为△ABC的“等周线”，则△ABC的所有“等周径”长为________．

Answer 1

【答案】或2或3．

【解析】

分三种情况：①当“等周线”经过点C时，直线交AB于点E；②当“等周线”经过点A时，直线交BC于点E，③当“等周线”经过点B时，直线交AC于点E．画图并运用勾股定理计算．

∵Rt△ABC中，∠C＝90°，AC＝4，BC＝3，

∴AB＝5

①如图，当“等周线”经过点C时，直线交AB于点E，设BE＝，则AE＝5-，作CH⊥AB于H．

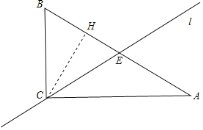
由题意得：3+＝4+5-

解得：＝3

∵CH＝

∴BH＝

∴EH＝3＝

在Rt△ECH中，CE＝

∴“等周径”长为；

②如图，当“等周线”经过点A时，直线交BC于点E，设BE＝，则CE＝3-

由题意得：4+3-＝5+

解得：＝1

∴EC＝2

在Rt△ACE中，AE

∴“等周径”长为；

③如图，当“等周线”经过点B时，直线交AC于点E，设AE＝，则CE＝4-

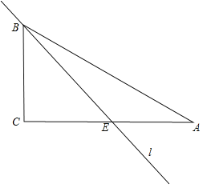
由题意得：3+4-＝5+

解得：＝1

∴CE＝3

在Rt△BCE中，BE＝＝

∴“等周径”长为．

综上所述，满足条件的“等周径”长为或或．

故答案为：或．