题目内容
【题目】如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.
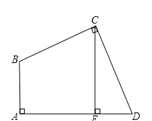
【答案】证明:如图,过点B作BF⊥CE于F,
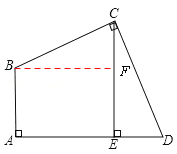
∵CE⊥AD,∴∠D+∠DCE=90°。
∵∠BCD=90°,∴∠BCF+∠DCE=90°。
∴∠BCF=∠D。
在△BCF和△CDE中,∵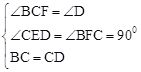 ,
,
∴△BCF≌△CDE(AAS)。∴BF=CE。
又∵∠A=90°,CE⊥AD,BF⊥CE,∴四边形AEFB是矩形。∴AE=BF。
∴AE=CE。
【解析】过点B作BF⊥CE于F,根据同角的余角相等求出∠BCF=∠D,再利用“角角边”证明△BCF和△CDE全等,根据全等三角形对应边相等可得BF=CE,再证明四边形AEFB是矩形,根据矩形的对边相等可得AE=BF,从而得证.

练习册系列答案
相关题目