题目内容
【题目】请完成下列的相似测试.
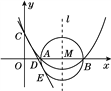
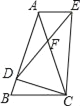
如图,在△ABC中,AB=AC=4,D是AB上一点,且BD=1,连接CD,然后作∠CDE=∠B,交平行于BC且过点A的直线于点E,DE交AC于点F,连接CE.
(1)求证:△AFD∽△EFC;
(2)试求AEBC的值.

【答案】(1)证明见解析;(2)AEBC=4.
【解析】试题分析:(1)证明△AEF∽△DCF,从而可得![]() ,再根据∠AFD=∠EFC,即可证明△AFD∽△EFC;
,再根据∠AFD=∠EFC,即可证明△AFD∽△EFC;
(2)证明△ACE∽△BCD,从而可推得AEBC=BDAC,再根据AC=4,BD=1,即可得AEBC=4.
试题解析:(1)∵AB=AC,
∴∠B=∠ACB,
又∵∠CDE=∠B,
∴∠CDE=∠ACB,
∵AE∥BC,
∴∠ACB=∠CAE,
∴∠CDE=∠CAE,
又∵∠AFE=∠DFC,
∴△AEF∽△DCF,
∴![]() ,即
,即![]() ,
,
又∵∠AFD=∠EFC,
∴△AFD∽△EFC;
(2)∵△AFD∽△EFC,
∴∠ACE=∠ADF,
又∵∠ADF+∠BDC=180°﹣∠FDC,∠BCD+∠BDC=180°﹣∠B,
而∠CDE=∠B,
∴∠ADF=∠BCD,
∴∠ACE=∠BCD,
又∵∠B=∠ACB=∠CAE,
∴△ACE∽△BCD,
∴![]() ,即AEBC=BDAC,
,即AEBC=BDAC,
∵AC=4,BD=1,
∴AEBC=1×4=4.

【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是 ;(精确到0.01)
(2)估算袋中白球的个数.