题目内容
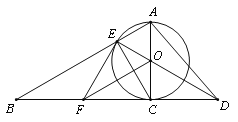
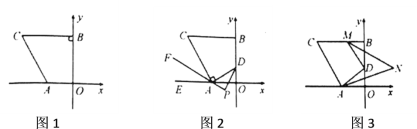
【题目】如图1,![]() 点是第二象限内一点,
点是第二象限内一点,![]() 轴于
轴于![]() ,且
,且![]() 是
是![]() 轴正半轴上一点,
轴正半轴上一点,![]() 是x轴负半
是x轴负半![]() 轴上一点,且
轴上一点,且![]() .
.
(1)![]() ( ),
( ),![]() ( )
( )
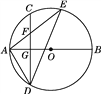
(2)如图2,设![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 时,
时,![]() 的角平分线与
的角平分线与![]() 的角平分线的反向延长线交于点
的角平分线的反向延长线交于点![]() ,求
,求![]() 的度数: (注: 三角形三个内角的和为
的度数: (注: 三角形三个内角的和为![]() )
)
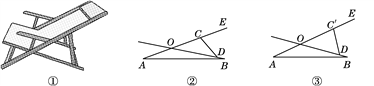
(3)如图3,当![]() 点在线段
点在线段![]() 上运动时,作
上运动时,作![]() 交
交![]() 于
于![]() 的平分线交于
的平分线交于![]() ,当
,当![]() 点在运动的过程中,
点在运动的过程中,![]() 的大小是否变化?若不变,求出其值;若变化,请说明理由.
的大小是否变化?若不变,求出其值;若变化,请说明理由.
【答案】(1)A(-2,0)、B(0,3);(2)∠APD=90°;(3)∠N的大小不变,∠N=45°
【解析】
(1)利用非负数的和为零,各项分别为零,求出a,b的值;
(2)如图,作DM∥x轴,结合题意可设∠ADP=∠OAP=x,∠EAF=∠CAF=∠OAP=y,根据平角的定义可知∠OAD=90°-2y,由平行线的性质可得∠OAD+∠ADM=180°,即90-2y+2x+90°=180°,进而可得出x=y,再结合图形即可得出∠APD的度数;
(3)∠N的大小不变,∠N=45°,如图,过D作DE∥BC,过N作NF∥BC,根据平行线的性质可知∠BMD+∠OAD=∠ADM=90°,然后根据角平分线的定义和平行线的性质,可得∠ANM=![]() ∠BMD+
∠BMD+![]() ∠OAD,据此即可得到结论.
∠OAD,据此即可得到结论.
(1)由![]() ,可得
,可得![]() 和
和![]() ,
,
解得![]()
∴A的坐标是(-2,0)、B的坐标是(0,3);
(2)如图,作DM∥x轴
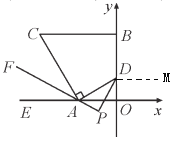
根据题意,设∠ADP=∠OAP=x,∠EAF=∠CAF=∠OAP=y,
∵∠CAD=90°,
∴∠CAE+∠OAD=90°,
∴2y+∠OAD=90°,
∴∠OAD=90°-2y,
∵DM∥x轴,
∴∠OAD+∠ADM=180°,
∴90-2y+2x+90°=180°,
∴x=y,
∴∠APD=180°-(∠PAD+∠ADP)=180°-(y+90°-2y+x)=180°-90°=90°
(3)∠N的大小不变,∠N=45°
理由:如图,过D作DE∥BC,过N作NF∥BC.
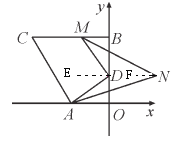
∵BC∥x轴,
∴DE∥BC∥x轴,NF∥BC∥x轴,
∴∠EDM=∠BMD,∠EDA=∠OAD,
∵DM⊥AD,
∴∠ADM=90°,
∴∠BMD+∠OAD=∠EDM+∠EDA=∠ADM=90°,
∵MN平分∠BMD,AN平分∠DAO,
∴∠BMN=![]() ∠BMD,∠OAN=
∠BMD,∠OAN=![]() ∠OAD,
∠OAD,
∴∠ANM=∠BMN+∠OAN=![]() ∠BMD+
∠BMD+![]() ∠OAD
∠OAD
=![]() ×90°=45°.
×90°=45°.

【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是 ;(精确到0.01)
(2)估算袋中白球的个数.