题目内容
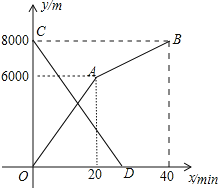
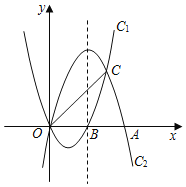
【题目】如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
(1)求抛物线C2的解析式;
(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.
【答案】(1)y=﹣x2+4x;(2)线段OC的长度![]() ;(3)S△MOC最大值为
;(3)S△MOC最大值为![]() .
.
【解析】
(1)C1、C2:y=ax2+bx开口大小相同、方向相反,则a=-1,将点A的坐标代入C2的表达式,即可求解;
(2)点A关于C2对称轴的对称点是点O(0,0),连接OC交函数C2的对称轴与点P,此时PA+PC的值最小,即可求解;
(3)S△MOC=![]() MH×xC=
MH×xC=![]() (-x2+4x-x)= -
(-x2+4x-x)= -![]() x2+
x2+![]() x,即可求解.
x,即可求解.
(1)令:y=x2﹣2x=0,则x=0或2,即点B(2,0),
∵C1、C2:y=ax2+bx开口大小相同、方向相反,则a=﹣1,
则点A(4,0),将点A的坐标代入C2的表达式得:
0=﹣16+4b,解得:b=4,
故抛物线C2的解析式为:y=﹣x2+4x;
(2)联立C1、C2表达式并解得:x=0或3,
故点C(3,3),
连接OC交函数C2的对称轴与点P,
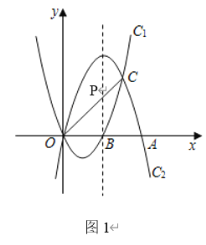
此时PA+PC的值最小为:线OC的长度![]() ;
;
设OC所在直线方程为:![]()
将点O(0,0),C(3,3)带入方程,解得k=1,
所以OC所在直线方程为:![]()
![]() 点P在函数C2的对称轴上,令x=2,带入直线方程得y=2,
点P在函数C2的对称轴上,令x=2,带入直线方程得y=2,
![]() 点P坐标为(2,2)
点P坐标为(2,2)
(3)由(2)知OC所在直线的表达式为:y=x,
过点M作y轴的平行线交OC于点H,
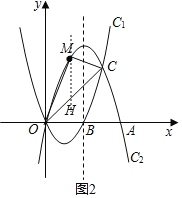
设点M(x,﹣x2+4x),则点H(x,x),则MH=﹣x2+4x﹣x
则S△MOC=S△MOH+S△MCH
=![]() MH×xC =
MH×xC = ![]() (﹣x2+4x﹣x)=
(﹣x2+4x﹣x)=![]()
∵△MOC的面积是一个关于x的二次函数,且开口向下
![]() 其顶点就是它的最大值。其对称轴为x=
其顶点就是它的最大值。其对称轴为x=![]() =
=![]() ,此时y=
,此时y=![]()
S△MOC最大值为![]() .
.