题目内容
【题目】如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD.BC上,且DE=BP=1.连接BE,EC,AP,DP,PD与CE交于点F,AP与BE交于点H.
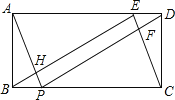
(1)判断△BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形,并证明你的判断;
(3)求四边形EFPH的面积.
【答案】(1)△BEC为直角三角形,理由见解析;(2)四边形EFPH是矩形,理由见解析;(3)![]()
【解析】
(1)根据矩形的性质可得∠BAE=∠CDE=90°,AB=CD=2,AD=BC=5,然后利用勾股定理即可求出BE和CE,然后根据勾股定理的逆定理即可证出△BEC为直角三角形;
(2)根据矩形的性质可得AD∥BC, AD=BC=5,然后根据平行四边形的判定定理可得四边形EBPD和四边形APCE均为平行四边形,从而证出四边形EFPH是平行四边形,然后根据矩形的定义即可得出结论;
(3)先利用三角形面积的两种求法,即可求出BH,从而求出HE,然后根据勾股定理即可求出HP,然后根据矩形的面积公式计算即可.
解:(1)△BEC为直角三角形,理由如下
∵四边形ABCD为矩形
∴∠BAE=∠CDE=90°,AB=CD=2,AD=BC=5
∵DE=1
∴AE=AD-DE=4
在Rt△ABE中,BE=![]()
在Rt△CDE中CE=![]()
∴BE2+CE2=25= BC2
∴△BEC为直角三角形
(2)四边形EFPH是矩形,理由如下
∵四边形ABCD为矩形
∴AD∥BC, AD=BC=5
∵DE=BP=1,
∴AD-DE=BC-BP=4
即AE=CP=4
∴四边形EBPD和四边形APCE均为平行四边形
∴EB∥DP,AP∥EC
∴四边形EFPH是平行四边形
∵△BEC为直角三角形,∠BEC=90°
∴四边形EFPH是矩形
(3)∵四边形APCE为平行四边形,四边形EFPH是矩形
∴AP=CE=![]() ,∠EHP=90°
,∠EHP=90°
∴∠BHP=180°-∠EHP=90°
∵S△ABP=![]()
∴![]()
解得:![]()
∴HE=BE-BH=![]()
在Rt△BHP中,HP =![]()
∴S矩形EFPH= HP·HE=![]()

【题目】近期江苏省各地均发布“雾霾”黄色预警,我市某口罩厂商生产一种新型口罩产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系满足下表.
销售单价x(元/件) | … | 20 | 25 | 30 | 40 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 20 | … |
(1)请你从所学过的一次函数、二次函数和反比例函数三个模型中确定哪种函数能比较恰当地表示y与x的变化规律,并直接写出y与x之间的函数关系式为__________;
(2)当销售单价为多少元时,厂商每月获得的利润为440万元?
(3)如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?