题目内容
【题目】已知一次函数y=﹣x+1与抛物线y=![]() x2+bx+c交于A(0,1),B两点,B点纵坐标为10,抛物线的顶点为C.
x2+bx+c交于A(0,1),B两点,B点纵坐标为10,抛物线的顶点为C.
(1)求b,c的值;
(2)判断△ABC的形状并说明理由;
(3)点D、E分别为线段AB、BC上任意一点,连接CD,取CD的中点F,连接AF,EF.当四边形ADEF为平行四边形时,求平行四边形ADEF的周长.

【答案】(1)b=2;(2)△ABC是直角三角形,理由见解析;(3)平行四边形ADEF周长为6+6![]() .
.
【解析】
(1)把A坐标代入抛物线解析式可求出c的值,把B的纵坐标代入直线解析式可求出其横坐标,再代入抛物线解析式即可求出b的值;
(2)△ABC的形状是直角三角形,分别作BG垂直于y轴,CH垂直于y轴,依次求∠BAG=45°,∠CAH=45°,进而得到∠CAB=90°;
(3)首先利用勾股定理易求AB的长,进而得到AC的长,利用三角形中位线的性质即可求出EF的长,再利用勾股定理即可求出AF的长,继而求出平行四边形ADEF的周长.
(1)把A(0,1),代入y=![]() x2+bx+c,
x2+bx+c,
解得c=1,
将y=10代入y=﹣x+1,得x=﹣9,
∴B点坐标为(﹣9,10),
将B (﹣9,10),代入y=![]() x2+bx+c
x2+bx+c
得b=2;
(2)△ABC是直角三角形,
理由如下:
∵y=![]() x2+2x+1=
x2+2x+1=![]() (x+3)2﹣2,
(x+3)2﹣2,
∴点C的坐标为(﹣3,﹣2),
分别作BG垂直于y轴,CH垂直于y轴
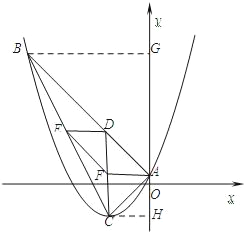
∵BG=AG=9,
∴∠BAG=45°,
同理∠CAH=45°,
∴∠CAB=90°
∴△ABC是直角三角形;
(3)∵BG=AG=9,
∴AB=9![]() ,
,
∵CH=AH=3,
∴AC=3![]() ,
,
∵四边形ADEF为平行四边形,
∴AD∥EF,
又∵F为CD中点,
∴CE=BE,
即EF为△DBC的中位线,EF
∴EF=AD=![]() BD,
BD,
∵AB=9![]() ,
,
∴EF=AD=3![]()
在Rt△ACD中,AD=3![]() ,AC=3
,AC=3![]() ,
,
∴CD=6,
∴AF=3,
∴平行四边形ADEF周长为6+6![]() .
.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案