��Ŀ����
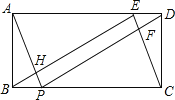
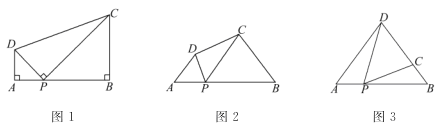
����Ŀ��(1)�����⣺��ͼ1�����ı���ABCD�У���PΪAB��һ�㣬��DPC=��A=��B=90������֤��AD��BC=AP��BP��
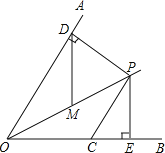
(2)��̽������ͼ2�����ı���ABCD�У���PΪAB��һ�㣬����DPC=��A=��B=��ʱ�����������Ƿ���Ȼ������˵�����ɣ�
(3)��Ӧ�ã������ã�1����2����õľ��������⣺
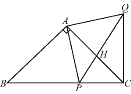
��ͼ3������ABD�У�AB=6��AD=BD=5����P��ÿ��1����λ���ȵ��ٶȣ��ɵ�A �������ر�AB���B�˶����������DPC=��A�����P���˶�ʱ��Ϊt���룩����DC�ij�����ABD�ױ��ϵĸ����ʱ����t��ֵ��
���𰸡���1��֤������������2�����۳���. (3)��t=1���5��.
�����������⣨1������DPC=��A=��B=90���ɵ���ADP=��BPC������֤����ADP�ס�BPC��Ȼ���������������ε����ʼ��ɽ�����⣻
��2������DPC=��A=��B=���ɵ���ADP=��BPC������֤����ADP�ס�BPC��Ȼ���������������ε����ʼ��ɽ�����⣻
��3������D��DE��AB�ڵ�E�����ݵ��������ε����ʿɵ�AE=BE=6�����ݹ��ɶ����ɵ�DE=8������ɵ�DC=DE=8������BC=10-8=2����֤��DPC=��A=��B������AD![]() BC=AP
BC=AP![]() BP���Ϳ����t��ֵ��
BP���Ϳ����t��ֵ��
�����������1����ͼ1��
�ߡ�DPC=��A=��B=90����
���ADP+��APD=90����
��BPC+��APD=90����
���APD=��BPC��
���ADP�ס�BPC��
��![]() ��
��
��AD![]() BC=AP
BC=AP![]() BP��
BP��
��2������AD![]() BC=AP
BC=AP![]() BP�Գ�����
BP�Գ�����
֤������ͼ2���ߡ�BPD=��DPC+��BPC��
���ߡ�BPD=��A+��APD��
���DPC+��BPC=��A+��APD��
�ߡ�DPC=��A=����
���BPC=��APD��
���ߡ�A=��B=����
���ADP�ס�BPC��
��![]() ��
��
��AD![]() BC=AP
BC=AP![]() BP��
BP��
��3������ͼ������D��DE��AB�ڵ�E��
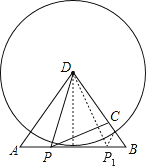
��AD=BD=10��AB=12��
��AE=BE=6
��DE=![]() =8��
=8��
����DΪԲ�ģ���DCΪ�뾶��Բ��AB���У�
��DC=DE=8��
��BC=10-8=2��
��AD=BD��
���A=��B��
���ߡ�DPC=��A��
���DPC=��A=��B��
�ɣ�1����2���ľ����ADBC=APBP��
����AP=t��BP=12-t��
��t��12-t��=10��2��
��t=2��t=10��
��t��ֵΪ2���10�룮

 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�