题目内容
【题目】已知一次函数
，当
时，
，则此函数与
轴的交点坐标是__________．
【答案】（0，
）或（0，
）
【解析】
根据k的取值分类讨论，①当k＞0时，y随x增大而增大，可知一次函数过
两点，利用待定系数法求出一次函数的解析式，然后将x=0代入即可求出此函数与
轴的交点坐标；②当k＜0时，y随x增大而减小，可知一次函数过
两点，利用待定系数法求出一次函数的解析式，然后将x=0代入即可求出此函数与轴的交点坐标．
解：①当k＞0时，y随x增大而增大
∵当
时，
∴一次函数过两点
将代入解析式中，得
解得：
故该一次函数的解析式为
将x=0代入，解得y=，
故此函数与轴的交点坐标是（0，）；
②当k＜0时，y随x增大而减小
∵当时，
∴一次函数过两点
将代入解析式中，得
解得：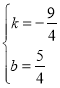
故该一次函数的解析式为
将x=0代入，解得y=，
故此函数与轴的交点坐标是（0，）；
综上所述：此函数与轴的交点坐标是（0，）或（0，）
故答案为：（0，）或（0，）．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
