Question

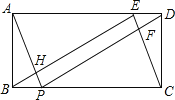
【题目】如图，一张矩形纸片ABCD，其中AD＝8cm，AB＝6cm，先沿对角线BD对折，点C落在点C′的位置，BC′交AD于点G．

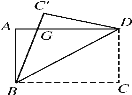
(1)求证：AG＝C′G；

(2) 求△BDG的面积．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）根据矩形的性质可得AD=BC，AB=DC，AD∥BC，∠BAD=90°，从而得出∠GDB=∠DBC，然后根据折叠的性质可得BC= BC′,∠GBD=∠DBC，从而得出AD= BC′，∠GBD=∠GDB，然后根据等角对等边可得GD=GB，即可证出结论；

（2）设GD=GB=x，利用勾股定理列出方程即可求出GD的长，然后根据三角形的面积公式求面积即可．

（1）证明：∵四边形ABCD为矩形

∴AD=BC，AB=DC，AD∥BC，∠BAD=90°

∴∠GDB=∠DBC

由折叠的性质可得BC= BC′,∠GBD=∠DBC

∴AD= BC′，∠GBD=∠GDB

∴GD=GB

∴AD－GD= BC′－GB

∴AG＝C′G；

（2）解：设GD=GB=x，则AG=AD－GD=8－x

在Rt△ABG中

即

解得：

即

∴S△BDG=