题目内容
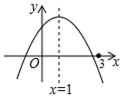
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②2a+b=0;③若m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中,正确结论的个数为( )
A.1B.2C.3D.4
【答案】B
【解析】
由抛物线的开口方向、对称轴位置、与y轴的交点位置判断出a、b、c与0的关系,进而判断①;根据抛物线对称轴为x=![]() =1判断②;根据函数的最大值为:a+b+c判断③;求出x=﹣1时,y<0,进而判断④;对ax12+bx1=ax22+bx2进行变形,求出a(x1+x2)+b=0,进而判断⑤.
=1判断②;根据函数的最大值为:a+b+c判断③;求出x=﹣1时,y<0,进而判断④;对ax12+bx1=ax22+bx2进行变形,求出a(x1+x2)+b=0,进而判断⑤.
解:①抛物线开口方向向下,则a<0,
抛物线对称轴位于y轴右侧,则a、b异号,即b>0,
抛物线与y轴交于正半轴,则c>0,
∴abc<0,故①错误;
②∵抛物线对称轴为直线x=![]() =1,
=1,
∴b=﹣2a,即2a+b=0,故②正确;
③∵抛物线对称轴为直线x=1,
∴函数的最大值为:a+b+c,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,故③错误;
④∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(﹣1,0)的右侧,
∴当x=﹣1时,y<0,
∴a﹣b+c<0,故④错误;
⑤∵ax12+bx1=ax22+bx2,
∴ax12+bx1﹣ax22﹣bx2=0,
∴a(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,
∴(x1﹣x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即x1+x2=﹣![]() ,
,
∵b=﹣2a,
∴x1+x2=2,故⑤正确.
综上所述,正确的是②⑤,有2个.
故选:B.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
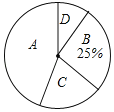
小学生10分钟应用题系列答案【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调査(问卷调査表如图所示),将调査结果整理后绘制例图1、图2两幅均不完整的统计图表.
最受欢迎的校本课程调查问卷
您好!这是一份关于您最喜欢的校本课程问卷调查表,请在表格中选择一个(只能选一个)您最喜欢的课程选项,在其后空格内打“√”,非常感谢您的合作.
选项 | 校本课程 | |
A | 3D打印 | |
B | 数学史 | |
C | 诗歌欣赏 | |
D | 陶艺制作 |
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B | 0.25 | |
C | 16 | b |
D | 8 | |
合计 | a | 1 |
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调査结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.