题目内容
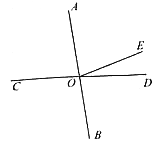
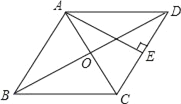
【题目】如图,已知菱形ABCD对角线交于点O,AE⊥CD于E,AE=OD,则∠CAE=_____.
【答案】30°
【解析】分析:由四边形ABCD为菱形,得到对角线互相垂直,进而得到一对直角相等,再由对顶角相等,得到△AFO与△DFE相似,利用相似三角形对应角相等得到一对角相等,利用ASA得到△AEC与△DOC全等,利用全等三角形对应边相等得到AC=CD,进而确定出△ACD为等边三角形,利用等边三角形的性质及三线合一性质即可求出所求角的度数.
详解:∵菱形ABCD, ∴AC⊥BD,AD=DC, ∵AE⊥CD, ∴∠AEC=∠DOC=90°,
∵∠AOD=∠AED=90°,∠AFO=∠DFE, ∴△AFO∽△DFE, ∴∠CAE=∠CDO,
∴△AEC≌△DOC(ASA), ∴AC=CD, ∴AC=CD=AD,即△ACD为等边三角形,
∵AE⊥CD, ∴AE为∠CAD的平分线, 则∠CAE=30°. 故答案为:30°.

练习册系列答案
相关题目