ΧβΡΩΡΎ»ί
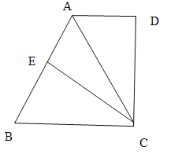
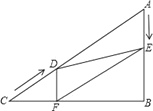
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœB=90ΓψΘ§AC=60cmΘ§ΓœA=60ΓψΘ§ΒψD¥”ΒψC≥ωΖΔ―ΊCAΖΫœρ“‘4cm/ΟκΒΡΥΌΕ»œρΒψA‘»ΥΌ‘ΥΕ·Θ§Ά§ ±ΒψE¥”ΒψA≥ωΖΔ―ΊABΖΫœρ“‘2cm/ΟκΒΡΥΌΕ»œρΒψB‘»ΥΌ‘ΥΕ·Θ§Β±Τδ÷–“ΜΗωΒψΒΫ¥ο÷’Βψ ±Θ§Νμ“ΜΗωΒψ“≤Υφ÷°ΆΘ÷Ι‘ΥΕ·Θ°…ηΒψDΓΔE‘ΥΕ·ΒΡ ±Φδ «tΟκΘ®0ΘΦtΓή15Θ©Θ°ΙΐΒψDΉςDFΓΆBC”ΎΒψFΘ§Ν§Ϋ”DEΘ§EFΘ°
Θ®1Θ©«σ÷ΛΘΚAE=DFΘΜ
Θ®2Θ©ΥΡ±Ώ–ΈAEFDΡήΙΜ≥…ΈΣΝβ–Έ¬πΘΩ»γΙϊΡήΘ§«σ≥ωtΒΡ÷ΒΘ§»γΙϊ≤ΜΡήΘ§ΥΒΟςάμ”…ΘΜ
Θ®3Θ©‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ΥΡ±Ώ–ΈBEDFΡήΖώΈΣ’ΐΖΫ–ΈΘΩ»τΡήΘ§«σ≥ωtΒΡ÷ΒΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©÷ΛΟςΦϊΫβΈωΘΜΘ®2Θ©Β±t=10 ±Θ§ΥΡ±Ώ–ΈAEFD «Νβ–ΈΘΜΘ®3Θ©ΥΡ±Ώ–ΈBEDF≤ΜΡήΈΣ’ΐΖΫ–ΈΘ§άμ”…ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©”…“―÷ΣΧθΦΰΩ…ΒΟRTΓςCDF÷–ΓœC=30ΓψΘ§Φ¥Ω…÷ΣDF=![]() CD=AE=2tΘΜ
CD=AE=2tΘΜ
Θ®2Θ©”…Θ®1Θ©÷ΣDFΓΈAE«“DF=AEΘ§Φ¥ΥΡ±Ώ–ΈADFE «ΤΫ––ΥΡ±Ώ–ΈΘ§»τΙΙ≥…Νβ–ΈΘ§‘ρΝΎ±ΏœύΒ»Φ¥AD=AEΘ§Ω…ΒΟΙΊ”ΎtΒΡΖΫ≥ΧΘ§«σΫβΦ¥Ω…÷ΣΘΜ
Θ®3Θ©ΥΡ±Ώ–ΈBEDF≤ΜΈΣ’ΐΖΫ–ΈΘ§»τΗΟΥΡ±Ώ–Έ «’ΐΖΫ–ΈΦ¥ΓœEDF=90ΓψΘ§Φ¥DEΓΈABΘ§¥Υ ±AD=2AE=4tΘ§ΗυΨίAD+CD=AC«σΒΟtΒΡ÷ΒΘ§ΦΧΕχΩ…ΒΟDFΓΌBFΘ§Ω…ΒΟ¥πΑΗΘ°
(1)ΓΏRtΓςABC÷–,ΓœB=90Γψ,ΓœA=60ΓψΘ§
ΓύΓœC=90ΓψΓœA=30Γψ.
”÷ΓΏ‘ΎRtΓςCDF÷–,ΓœC=30ΓψΘ§CD=4t
ΓύDF=![]() CD=2tΘ§
CD=2tȧ
ΓύDF=AEΘΜ
(2)ÿDFøABȧDF=AEȧ
ΓύΥΡ±Ώ–ΈAEFD «ΤΫ––ΥΡ±Ώ–ΈΘ§
Β±AD=AE ±Θ§ΥΡ±Ώ–ΈAEFD «Νβ–ΈΘ§
Φ¥604t=2tΘ§ΫβΒΟΘΚt=10Θ§
Φ¥Β±t=10 ±Θ§ΥΡ±Ώ–ΈAEFD «Νβ–ΈΘΜ
(3)ΥΡ±Ώ–ΈBEDF≤ΜΡήΈΣ’ΐΖΫ–ΈΘ§άμ”…»γœ¬ΘΚ
Β±ΓœEDF=90Γψ ±,DEΓΈBC.
ΓύΓœADE=ΓœC=30Γψ
ΓύAD=2AE
ÿCD=4tȧ
ΓύDF=2t=AEΘ§
ΓύAD=4tΘ§
Γύ4t+4t=60Θ§
Γύt=![]() ±,ΓœEDF=90Γψ
±,ΓœEDF=90Γψ
ΒΪBFΓΌDFΘ§
ΓύΥΡ±Ώ–ΈBEDF≤ΜΩ…ΡήΈΣ’ΐΖΫ–ΈΓΘ