题目内容
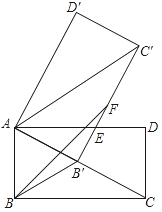
【题目】如图,在△ABC中,∠ABC=90°,∠BAC=60°,AC绕点C顺时针旋转60°至CD,F是CD的中点,连接BF交AC于点E,连接AD.
求证:(1)AC=BF;
(2)四边形ABFD是平行四边形.
【答案】证明见解析
【解析】
(1)连接AF,由旋转的旋转得到AC=DC,∠ACD=60°,进而△ACD是等边三角形,再证四边形ADCF是矩形,根据矩形的对角线相等即可得到AC=BF.
(2)根据△ACD是等边三角形,得到AC=AD,进一步证明AD=BF,再证明AB=DF,即可得到四边形ABFD是平行四边形.
(1)如图,连接AF.
∵AC绕点C顺时针旋转60°至CD,∴AC=DC,∠ACD=60°,∴△ACD是等边三角形.
∵F是CD的中点,∴AF⊥CD,∴∠AFC=90°.
∵在△ABC中,∠ABC=90°,∠BAC=60°,∴∠ACD=30°.
∵∠ACD=60°,∴∠BCD=90°.
又∵∠ADC=90°,∴四边形ADCF是矩形,∴AC=BF.
(2)∵△ACD是等边三角形,∴AC=AD.
∵AC=BF,∴AD=BF.
∵四边形ABCF是矩形,∴AB=CF.
∵F是CD的中点,∴DF=CF,∴AB=DF,∴四边形ABFD是平行四边形.

练习册系列答案
相关题目