ЬтФПФкШн
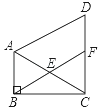
ЁОЬтФПЁПЮЪЬтБГОАЃКЮвУЧбЇЯАЕШБпШ§НЧаЮЪБЕУЕНжБНЧШ§НЧаЮЕФвЛИіаджЪЃКдкжБНЧШ§НЧаЮжаЃЌШчЙћвЛИіШёНЧЕШгк30ЁуЃЌФЧУДЫќЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЃЎМДЃКШчЭМ1ЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЁЯABC=30ЁудђЃКAC=![]() ABЃЎ
ABЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌСЌНгABБпЩЯжаЯпCFЃЌЪдЫЕУїЁїACFЮЊЕШБпШ§НЧаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЕуDЪЧБпCBбгГЄЯпЩЯвЛЕуЃЌСЌНгADЃЌзїЕШБпЁїADEЃЌЧвЕуEдкЁЯACBЕФФкВПЃЌСЌНгBEЃЌEFЃЎЪдЫЕУїEFЁЭAB.

ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнШ§НЧаЮФкНЧКЭЖЈРэЕУЕНЁЯA=60ЁуЃЌИљОнЕШБпШ§НЧаЮЕФХаЖЈЖЈРэжЄУїЃЛ
ЃЈ2ЃЉжЄУїЁїCADЁеЁїFAEЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНЁЯEFA=ЁЯBCA=90ЁуЃЌИљОнДЙжБЕФЖЈвхжЄУїЃЛ
ЃЈ1ЃЉжЄУїЃКЁпЁЯACB=90ЁуЃЌЁЯABC=30ЁуЃЌ
ЁрЁЯA=60ЁуЃЌ
ЁпCF=![]() AB=AFЃЌЁЯA=60ЁуЃЌ
AB=AFЃЌЁЯA=60ЁуЃЌ
ЁрЁїACFЮЊЕШБпШ§НЧаЮЃЛ
ЃЈ2ЃЉжЄУїЃКЁпЁїACFЮЊЕШБпШ§НЧаЮЃЌ
ЁрAC=AFЃЌ
ЁпЁїADEЪЧЕШБпШ§НЧаЮЃЌ
ЁрAD=AE=DEЃЌЁЯDAE=60ЁуЃЌ
ЁрЁЯCAB+ЁЯBAD=ЁЯDAE+ЁЯBADЃЌМДЁЯCAD=ЁЯBAEЃЌ
дкЁїCADКЭЁїFAEжаЃЌ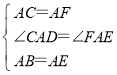 ЃЌ
ЃЌ
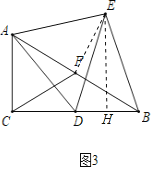
ЁрЁїCADЁеЁїFAEЃЈSASЃЉЃЌ
ЁрЁЯEFA=ЁЯBCA=90ЁуЃЌМДEFЁЭABЃЛ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ