题目内容
【题目】△ABC在平面直角坐标系中的位置如图所示.
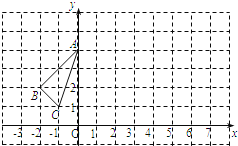
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某条直线对称?若是,请在图上画出这条对称轴.
【答案】(1)见解析;(2)见解析,A2(6,4),B2(4,2),C2(5,1);(3)△A1B1C1和△A2B2C2是轴对称图形,对称轴为图中直线l:x=3,见解析.
【解析】
(1)根据轴对称图形的性质,找出A、B、C的对称点A1、B1、C1,画出图形即可;
(2)根据平移的性质,△ABC向右平移6个单位,A、B、C三点的横坐标加6,纵坐标不变;
(3)根据轴对称图形的性质和顶点坐标,可得其对称轴是l:x=3.
(1)由图知,A(0,4),B(﹣2,2),C(﹣1,1),∴点A、B、C关于y轴对称的对称点为A1(0,4)、B1(2,2)、C1(1,1),连接A1B1,A1C1,B1C1,得△A1B1C1;
(2)∵△ABC向右平移6个单位,∴A、B、C三点的横坐标加6,纵坐标不变,作出△A2B2C2,A2(6,4),B2(4,2),C2(5,1);
(3)△A1B1C1和△A2B2C2是轴对称图形,对称轴为图中直线l:x=3.


【题目】在3月22日的“世界水资源保护日”当天,我县某校开展“节约用水,从你我做起”的宣传活动,小明利用课余时间对他所居住小区100户居民2月份的用水量进行调查,情况如下表
用水量(m3) | 9 | 10 | 11 | 12 |
户数(户) | 20 | 40 | 30 | 10 |
请根据表中的数据,求这100户居民2月份用水量的众数、中位数和平均数.
【题目】小聪在用描点法画二次函数y=ax2+bx+c![]() 的图象时,列出下面的表格:
的图象时,列出下面的表格:
x | … | -5 | -4 | -3 | -2 | -1 | … |
y | … | -7.5 | -2.5 | 0.5 | 1.5 | 0.5 | … |
根据表格提供的信息,下列说法错误的是( ).
A. 该抛物线的对称轴是直线x=-2![]()
B. b2-4ac>0![]()
C. 该抛物线与y![]() 轴的交点坐标为(0,-3.5)
轴的交点坐标为(0,-3.5)
D. 若(0.5,y1)![]() 是该抛物线上一点.则y1<-2.5
是该抛物线上一点.则y1<-2.5![]()