Question

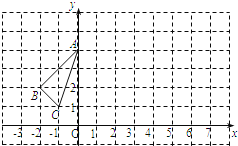
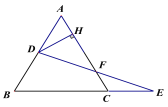
【题目】如图，在△ABC中，∠ABC=45°，F是高AD和BE的交点，CD=4，则线段DF的长为（ ）

A.4B.5C.6D.8

Answer 1

【答案】A

【解析】

求出利用等腰三角形性质得到，AD=BD，根据∠FBD+∠C=90°，∠CAD+∠C=90°，推出∠FBD=∠CAD，根据ASA证△FBD≌△CAD，推出CD=DF即可．

解：∵AD是△ABC的高，
∴AD⊥BC，
∴∠ADB=∠ADC=90°，
∵∠ABC=45°，
∴∠BAD=45°=∠ABD，
∴AD=BD，
∵BE⊥AC，
∴∠BEC=90°，
∴∠FBD+∠C=90°，∠CAD+∠C=90°，
∴∠FBD=∠CAD，
在△FBD和△CAD中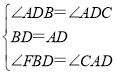
，
∴△FBD≌△CAD（ASA），
∴CD=DF=4，
所以选A