题目内容
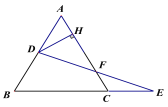
【题目】如图,△ABC中,AB=AC,且∠ABC=60°,D为△ABC内一点 ,且DA=DB,E为△ABC外一点,BE=AB,且∠EBD=∠CBD,连DE,CE. 下列结论:①∠DAC=∠DBC;②BE⊥AC ;③∠DEB=30°. 其中正确的是( )
A.①...B.①③...C.② ...D.①②③
【答案】B
【解析】
连接DC,证![]() ,再证
,再证![]() ,得出
,得出![]() ;其它两个条件运用假设成立推出答案即可.
;其它两个条件运用假设成立推出答案即可.
解:证明:连接DC,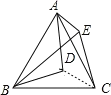
∵△ABC是等边三角形,
∴AB=BC=AC,∠ACB=60°,
∵DB=DA,DC=DC,
在△ACD与△BCD中,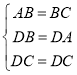 ,
,
∴△ACD≌△BCD (SSS),
由此得出结论①正确;
∴∠BCD=∠ACD=![]()
∵BE=AB,
∴BE=BC,
∵∠DBE=∠DBC,BD=BD,
在△BED与△BCD中,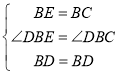 ,
,
∴△BED≌△BCD (SAS),
∴∠DEB=∠BCD=30°.
由此得出结论③正确;
∵EC∥AD,
∴∠DAC=∠ECA,
∵∠DBE=∠DBC,∠DAC=∠DBC,
∴设∠ECA=∠DBC=∠DBE=∠1,
∵BE=BA,
∴BE=BC,
∴∠BCE=∠BEC=60°+∠1,
在△BCE中三角和为180°,
∴2∠1+2(60°+∠1)=180°
∴∠1=15°,
∴∠CBE=30,这时BE是AC边上的中垂线,结论②才正确.
因此若要结论②正确,需要添加条件EC∥AD.
故答案为:B.

练习册系列答案
相关题目
【题目】八(1)班组织了一次食品安全知识竞赛,甲、乙两队各5人的成绩如表所示(10分制).
数据 | 中位数 | 众数 | 方差 | |||||
甲 | 8 | 10 | 9 | 6 | 9 | 9 | 1.84 | |
乙 | 10 | 8 | 9 | 7 | 8 | 8 | 1.04 | |
(1)补全表格中的众数和中位数
(2)并判断哪队的成绩更稳定?为什么?