��Ŀ����
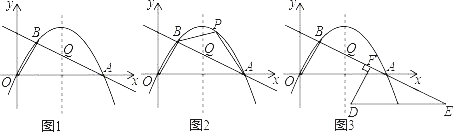
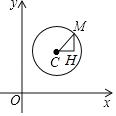
����Ŀ����ƽ��ֱ������ϵ�У���C��x0��y0��ΪԲ�İ뾶Ϊr��Բ�ı������ǣ�x��x0��2+��y��y0��2��r2�����磬��ƽ��ֱ������ϵ�У���C��Բ��C��2��3������M��3��5����Բ��һ�㣬��ͼ������C����M�ֱ���x�ᡢy���ƽ���ߣ����ڵ�H����Rt��MCH�У��ɹ��ɶ����ɵã�r2��MC2��CH2+MH2��1+4��5����ԲC�ı������ǣ�x��2��2+��y��3��2��5����ô�Ե㣨��3��4��ΪԲ�ģ����㣨��2����1����Բ�ı�������_____��
���𰸡�26
��������
����ͼ������������ȷ��Բ�ı����̵Ľ���ʽ�ǣ�x��x0��2+��y��y0��2��r2�����У�x0��y0����Բ�ģ�r��MC֮��ľ��룬���ù��ɶ������r�ij��ȼ��ɽ���.
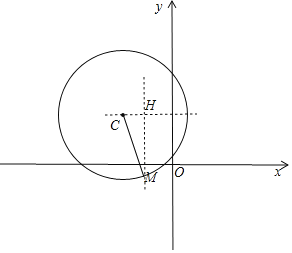
�⣺��ͼ��Բ��C����3��4������M����2����1������C��CH��x�ᣬ��M��MH��y�ᣬCH��MH�ڵ�H��
����Rt��MCH��CH����2������3����1��MH��4������1����5��
��r2��MC2��CH2+MH2��1+25��26��
���Ե㣨��3��4��ΪԲ�ģ����㣨��2����1����Բ�ı������ǣ�x+3��2+��y��4��2��26��
�ʴ�Ϊ����x+3��2+��y��4��2��26��

��ϰ��ϵ�д�
 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
�����Ŀ