题目内容
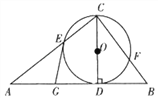
【题目】如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA, CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.
【答案】证明见解析
【解析】试题分析: (证法一): 连接OE,DE根据已知条件可证得∠1=∠2,∠3=∠4,再由∴∠1+∠3=∠2+∠4 ,即可证得∠OEG=∠ODG=90°,结论得证;(证法二):连接OE,OG,证得OG∥AC,根据平行线的性质可得∠1=∠2,∠3=∠4,根据等腰三角形的的性质可得∠2=∠4,即可得∠1=∠3,利用SAS证得△OEG≌△ODG,即可得∠OEG=∠ODG=90°,结论得证.
试题解析:
(证法一)
证明:连接OE,DE ,
∵CD是⊙O的直径,
∴∠AED=∠CED=90°,
∵G是AD的中点,
∴EG=![]() AD=DG,∴∠1=∠2;
AD=DG,∴∠1=∠2;
∵OE=OD,∴∠3=∠4 ,
∴∠1+∠3=∠2+∠4 ,
∴∠OEG=∠ODG=90°,
故GE是⊙O的切线。
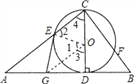
(证法二)
证明:连接OE,OG,
∵AG=GD,CO=OD,
∴OG∥AC ,
∴∠1=∠2,∠3=∠4.
∵OC=OE,∴∠2=∠4,
∴∠1=∠3 ,
又OE=OD,OG=OG,
∴△OEG≌△ODG,
∴∠OEG=∠ODG=90°,
∴GE是⊙O的切线.

练习册系列答案
相关题目
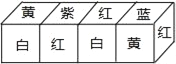
【题目】把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
现将上述大小相同,颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体,如图所示,那么长方体的下底面共有_____朵花.