题目内容
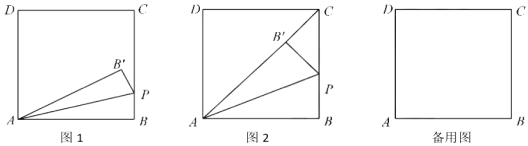
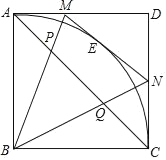
【题目】如图,正方形ABCD的边长为1,点E是弧AC上的一个动点,过点E的切线与AD交于点M.与CD交于点N.
(1)求证:∠MBN=45°;
(2)设AM=x,CN=y,求y关于x的函数关系式;
(3)设正方形的对角线AC交BM于P,BN于Q,如果AP=m,CQ=n,求m与n之间满足的关系式.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接BE,证明Rt△ABM≌Rt△EBM(HL),即可得∠ABM=∠EBM,再证明Rt△CBN≌Rt△EBN,即可证明∠CBN=∠EBN,再根据∠ABM+∠EBM+∠EBN+∠CBN=90°,即可证明∠MBN=45°.
(2)根据(1)得MN=x+y,MD=1﹣x,ND=1﹣y.再根据勾股定理列方程化简即可得到y关于x的函数关系式.
(3)根据△ABQ∽△BPQ和△CBP∽△BQP列出相似比,再根据相似比可得![]() ,代入计算即可.
,代入计算即可.
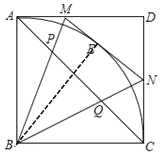
证明:(1)如图,连接BE,
∵MN是⊙B的切线
∴BE⊥MN,
∵AB=BE,BM=BM
∴Rt△ABM≌Rt△EBM(HL)
∴∠ABM=∠EBM,
同理可证:Rt△CBN≌Rt△EBN
∴∠CBN=∠EBN
∵∠ABC=90°
∴∠ABM+∠EBM+∠EBN+∠CBN=90°
∴2(∠MBE+∠NBE)=90°
∴∠MBN=45°
(2)∵Rt△ABM≌Rt△EBM,Rt△CBN≌Rt△EBN
∴AM=ME=x,CN=NE=y
∴MN=x+y,MD=1﹣x,ND=1﹣y
∵MD2+ND2=MN2,
∴(1﹣x)2+(1﹣y)2=(x+y)2,
∴1﹣2x+1﹣2y=2xy
∴y=![]()
(3)∵四边形ABCD是正方形
∴AB=BC=1,∠BAC=∠ACB=45°
∴AC=![]()
∵∠MBN=∠BAC=45°,∠AQB=∠AQB
∴△ABQ∽△BPQ
∴![]()
∴![]() ①
①
∵∠MBN=∠ACB=45°,∠CPB=∠BPQ
∴△CBP∽△BQP
∴![]()
∴![]() ②
②
由①②得:![]()
∴AC﹣CQ=![]()
∴![]() ﹣n=
﹣n=![]()
∴m=![]()

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
满意度 | 人数 | 所占百分比 |
非常满意 | 12 | 10% |
满意 | 54 | m |
比较满意 | n | 40% |
不满意 | 6 | 5% |
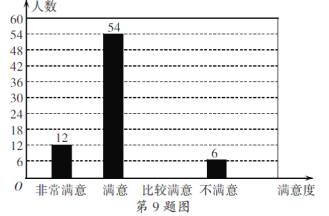
根据图表信息,解答下列问题:
(1)本次调查的总人数为______,表中m的值为_______;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.