题目内容
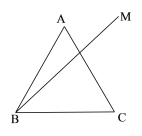
【题目】如图,等边△ABC中,BM是ABC内部的一条射线,且![]() ,点A关于BM的对称点为D,连接AD,BD,CD,其中AD、CD的延长线分别交射线BM于点E,P.
,点A关于BM的对称点为D,连接AD,BD,CD,其中AD、CD的延长线分别交射线BM于点E,P.
(1)依题意补全图形;
(2)若ABM ,求BDC 的大小(用含的式子表示);
(3)用等式表示线段PB,PC与PE之间的数量关系,并证明.
【答案】(1)见解析;(2) 60°+![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)正确画图;
(2)根据对称得:BM是AD的垂直平分线,则BA=BD,根据等腰三角形的性质和等边三角形可得结论;
(3)在射线PD上截取PF使PF=PB,连接BF,如图,先证明△BPF是等边三角形,再证明△BFC≌△BPD,则CF=PD=2PE.根据线段的和可得结论.
(1)如图所示:
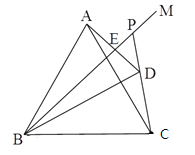
(2∵点A与点D关于BM对称,∴BM是AD的垂直平分线,∴BA=BD.
∵∠ABM=α,∴∠ABD=2∠ABM=2α.
∵等边△ABC,∴BA=CB=BD,∠ABC=60°,∴∠DBC=∠ABC-∠ABD =60°-![]() ,∴∠BDC=∠DCB=
,∴∠BDC=∠DCB=![]() (180°
(180°![]() ∠DBC)=60°+
∠DBC)=60°+![]() .
.
(3)结论:PB=PC+2PE.证明如下:
在射线PD上截取PF使PF=PB,连接BF.
∵BA=BD,∠ABD=![]() ,∴∠BDA=∠BAD=90°
,∴∠BDA=∠BAD=90°![]()
![]() .
.
∵∠BDC=60°+![]() ,∴∠PDE=180-(∠BDA+∠BDC)=30°.
,∴∠PDE=180-(∠BDA+∠BDC)=30°.
∵∠DEP=90°,∴PD=2PE.
∵∠BPF=∠DPE=90°![]() ∠PDE=60°,PF=PB,∴△BPF是等边三角形,∴∠BPF=∠BFP=60°.
∠PDE=60°,PF=PB,∴△BPF是等边三角形,∴∠BPF=∠BFP=60°.
∵∠BDC=∠DCB,∴∠BDP=∠BCF.
在△BFC和△BPD中,∵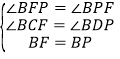 ,∴△BFC≌△BPD,∴CF=PD=2PE,∴PB= PC+BF=PC+2PE.
,∴△BFC≌△BPD,∴CF=PD=2PE,∴PB= PC+BF=PC+2PE.

 名校课堂系列答案
名校课堂系列答案【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
【题目】研学基地高明盈香生态园的团体票价格如下表:
数量(张) | 30~50 | 51~100 | 101及以上 |
单价(元/张) | 80 | 60 | 50 |
某校七年级(1)、(2)班共102人去研学,其中(1)班人数较少,不足50人,两个班相差不超过20人。经估算,如果两个班都以班为单位购票,则一共应付7080元,问:
(1)两个班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可省多少钱?