题目内容
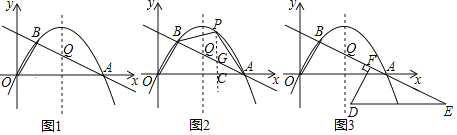
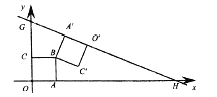
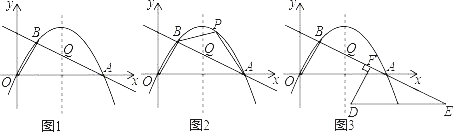
【题目】如图1,在平面直角坐标系中,O是坐标原点.点A在x轴的正半轴上,点A的坐标为(10,0).一条抛物线![]() 经过O,A,B三点,直线AB的表达式为
经过O,A,B三点,直线AB的表达式为![]() ,且与抛物线的对称轴交于点Q.
,且与抛物线的对称轴交于点Q.
(1)求抛物线的表达式;
(2)如图2,在A,B两点之间的抛物线上有一动点P,连结AP,BP,设点P的横坐标为m,△ABP的面积S,求出面积S取得最大值时点P的坐标;
(3)如图3,将△OAB沿射线BA方向平移得到△DEF,在平移过程中,以A,D,Q为顶点的三角形能否成为等腰三角形?如果能,请直接写出此时点E的坐标(点O除外);如果不能,请说明理由.
【答案】(1)![]() ;(2)当S取得最大值16时,点P的坐标为(6,6);(3)以A,D,Q为顶点的三角形能成为等腰三角形,点E坐标为:E1(21,
;(2)当S取得最大值16时,点P的坐标为(6,6);(3)以A,D,Q为顶点的三角形能成为等腰三角形,点E坐标为:E1(21,![]() ),E2(15,
),E2(15,![]() ),E3(
),E3(![]() ),E4(16,﹣3).
),E4(16,﹣3).
【解析】
(1)将点A的坐标(10,0).O(0,0)代入抛物线![]() ,解出b,c,再代回,即可得抛物线的解析式;
,解出b,c,再代回,即可得抛物线的解析式;
(2)先将直线与抛物线解析式联立,解出点B坐标,再设出点P和点G坐标,用相关点的横纵坐标表示线段长河高,从而可得面积的表达式,再从函数角度即可得解;
(3)利用勾股定理分别表示出AD2,AQ2,QD2,再分AD=AQ,AD=QD,AQ=QD,分别来求解,从而得点D坐标,再将其横坐标加10,纵坐标不变即可得点E的坐标.
解:(1)∵抛物线![]() 经过O,A,B三点,点A的坐标为(10,0).O(0,0),
经过O,A,B三点,点A的坐标为(10,0).O(0,0),
∴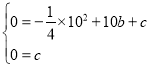
∴![]() ,
,
∴抛物线的表达式为:y=﹣![]() x2+
x2+![]() x.
x.
(2)由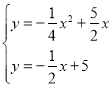 得﹣
得﹣![]() x2+
x2+![]() x=
x=![]() ,
,
∴x=2或x=10,
∴点B(2,4).
如图2,作PC⊥x轴于C点,交AB于点G,
∵动点P在抛物线上,直线AB的表达式为![]() ,
,
∴设P(m,﹣![]() m2+
m2+![]() m),G(m,
m),G(m,![]() ),
),
∴PG=﹣![]() m2+3m﹣5,
m2+3m﹣5,
∴S=![]() PG(xA﹣xG)+
PG(xA﹣xG)+![]() PG(xG﹣xB)=
PG(xG﹣xB)=![]() (﹣
(﹣![]() m2+3m﹣5)(10﹣2)=﹣m2+12m﹣20=﹣(m﹣6)2+16,
m2+3m﹣5)(10﹣2)=﹣m2+12m﹣20=﹣(m﹣6)2+16,
∴当m=6时,S最大=16,
∴P(6,6)
答:当S取得最大值时点P的坐标为(6,6).
(3)∵抛物线的对称轴为x=5,点Q在直线![]() 上,
上,
∴Q点坐标为(5,![]() ),D点在过O点且平行于AB的直线y=
),D点在过O点且平行于AB的直线y=![]() 上,设D(a,
上,设D(a,![]() ),
),
∴AD2=(10﹣a)2+![]() a2,AQ2=25+
a2,AQ2=25+![]() =
=![]() ,QD2=(a﹣5)2+
,QD2=(a﹣5)2+![]()
①当AD=AQ时,(10﹣a)2+![]() a2=
a2=![]() ,解得a1=11,a2=5,
,解得a1=11,a2=5,
∴D1(11,![]() ),D2(5,﹣
),D2(5,﹣![]() );
);
∴E1(21,![]() ),E2(15,-
),E2(15,-![]() );
);
②当AD=QD时,(10﹣a)2+![]() a2=(a﹣5)2+
a2=(a﹣5)2+![]() ,解得a=
,解得a=![]() ,
,
∴D3(![]() ,
,![]() ),E3(
),E3(![]() ,
,![]() );
);
③当AQ=QD时,![]() =(a﹣5)2+
=(a﹣5)2+![]() ,解得a=6,
,解得a=6,
∴D4(6,﹣3),E4(16,﹣3)
综上所述,以A,D,Q为顶点的三角形能成为等腰三角形,点E坐标为:E1(21,![]() ),E2(15,
),E2(15,![]() ),E3(
),E3(![]() ,
,![]() ),E4(16,﹣3).
),E4(16,﹣3).