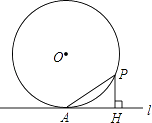题目内容
【题目】在四边形ABCD中,AB=AD,BC=CD.
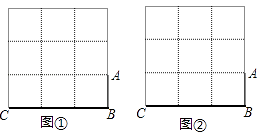
(1)如图1,请连接AC,BD,求证:AC垂直平分BD;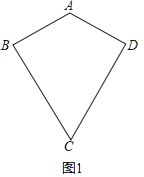
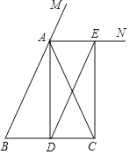
(2)如图2,若∠BCD=60°,∠ABC=90°,E,F分别为边BC,CD上的动点,且∠EAF=60°,AE,AF分别与BD交于G,H,求证:△AGH∽△AFE;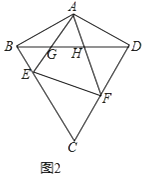
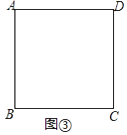
(3)如图3,在(2)的条件下,若 EF⊥CD,直接写出 ![]() 的值.
的值.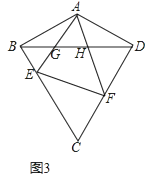
【答案】
(1)解:证明:如图1中,连接BD、AC.
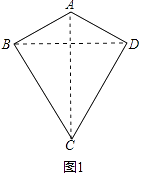
∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴AC是线段BD的垂直平分线,
即AC垂直平分线段BD.
(2)解:如图2中,将△ABE绕点A逆时针旋转120得到△ADM.连接AC交BD于O.
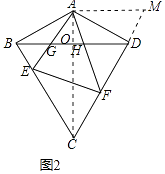
∵B、D关于AC对称,
∴∠ABC=∠ADC=90°,
∵∠BCD=60°,
∴∠BAD=120°,
∵∠EAF=60°,
∴∠BAE+∠DAF=∠DAF+∠DAM=60°,
∴∠FAE=∠FAM,
∵∠ADM=∠ABE=90°=∠ADF,
∴F、D、M共线,
∵FA=FA,AE=AM,
∴△FAE≌△FAM,
∴∠AFE=∠AFM,
∵∠CAD=∠CAB=60°=∠EAF,
∴∠GAO=∠DAF,
∵∠AGO+∠GAO=90°,∠AFD+∠FAD=90°,
∴∠AGO=∠ADF,
∴∠AGH=∠AFE,∵∠GAH=∠FAE,
∴△AGH∽△AFE.
(3)解:如图3中,连接AC交BD于O,作HM⊥AD于M.
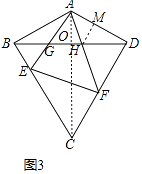
∵EF⊥CD,
∴∠EFD=90°,
由(2)可知∠AFD=∠AFE=∠AGO=45°,
∵∠ADF=90°,
∴AD=DF,设HM=AM=a,则DH=2a,DM= ![]() a,
a,
在Rt△ACD中,∵∠ACD=30°,AD=(1+ ![]() )a,
)a,
∴CD=BD= ![]() AD=(3+
AD=(3+ ![]() )a,
)a,
在Rt△AHD中,∵∠ADH=30°,AD=(1+ ![]() )a,
)a,
∴AO=OG= ![]() AD=
AD= ![]() a,OD=
a,OD= ![]() OA=
OA= ![]() a,
a,
∴OH=OD﹣DH= ![]() a﹣2a=
a﹣2a= ![]() a,
a,
∴GH=OG+OH= ![]() a,
a,
∴ ![]() =
= ![]() =
= ![]() .
.
【解析】(1)利用垂直平分线的判定定理及两点确定一条直线可证出;(2)通过旋转构造全等三角形,即△FAE≌△FAM,进而得出∠AFE=∠AFM,∠GAH=∠FAE,证出相似;(3)利用(2)的结论得出∠ADF=90°,AD=DF,设出参数HM=AM=a,运用三角函数定义,用a的代数式分别表示出BD,GH,可求出比值.
【考点精析】本题主要考查了相似三角形的判定与性质和锐角三角函数的定义的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能正确解答此题.

 口算题天天练系列答案
口算题天天练系列答案【题目】某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表.
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
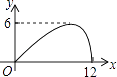
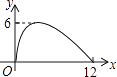
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,求工厂的最大利润?