题目内容
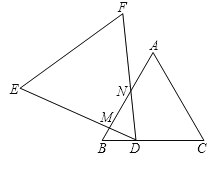
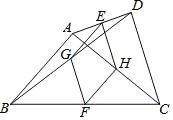
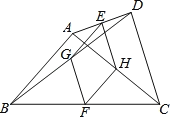
【题目】如图,在四边形ABCD中,AB=CD,E、F、G、H分别为AD、BC、BD、AC的中点,顺次连接E、G、F、H.
(1)猜想四边形EGFH是什么特殊的四边形,并说明理由;
(2)当∠ABC与∠DCB满足什么关系时,四边形EGFH为正方形,并说明理由;
(3)猜想:∠GFH、∠ABC、∠DCB三个角之间的关系.直接写出结果____________.
【答案】(1)菱形;(2)∠ABC+∠DCB=90°;(3)∠GFH+∠ABC+∠DCB=180°或∠GFH+∠ABC-∠DCB=180°
【解析】
(1)根据三角形中位线的性质得到EG![]() AB,EH
AB,EH![]() CD,HF
CD,HF![]() AB,EG∥AB,HF∥AB,根据菱形的判定定理即可得到结论;
AB,EG∥AB,HF∥AB,根据菱形的判定定理即可得到结论;
(2)根据平行线的性质得到∠ABC=∠HFC,∠DCB=∠GFB,根据平角的定义得到∠GFH=90°,于是得到结论;
(3)由平行线的性质得到∠ABC=∠HFC,∠DCB=∠GFB,根据平角的定义即可得到结论.
(1)四边形EGFH是菱形.理由如下:
∵E、F、G、H分别为AD、BC、BD、AC的中点,
∴EG![]() AB,EH
AB,EH![]() CD,HF
CD,HF![]() AB,EG∥AB,HF∥AB,
AB,EG∥AB,HF∥AB,
∴四边形EGFH是平行四边形,EG=EH,
∴四边形EGFH是菱形;
(2)当∠ABC+∠DCB=90°时,四边形EGFH为正方形,
理由:∵GF∥CD,HF∥AB,
∴∠ABC=∠HFC,∠DCB=∠GFB.
∵∠ABC+∠DCB=90°,
∴∠GFH=90°,
∴菱形EGFH是正方形;
(3)当∠ABC+∠DCB<180°时,∠GFH+∠ABC+∠DCB=180°.
理由如下:
∵GF∥CD,HF∥AB,
∴∠ABC=∠HFC,∠DCB=∠GFB.
∵∠BFG+∠GFH+∠HFC=180°,
∴∠GFH+∠ABC+∠DCB=180°.
当∠ABC+∠DCB=180°时,∠GFH=0°,四边形EGFH不存在,∠GFH+∠ABC+∠DCB=180°;
当∠ABC+∠DCB>180°时,∠GFH+∠ABC﹣∠DCB=180°.
综上所述:∠GFH+∠ABC+∠DCB=180°或∠GFH+∠ABC-∠DCB=180°.

 名校课堂系列答案
名校课堂系列答案【题目】某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表.
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,求工厂的最大利润?