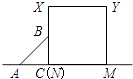题目内容
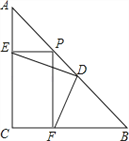
【题目】在△ABC中,∠C=90°,AC=BC=3,D为AB的中点,点P是AB上的一个动点,PE⊥AC于点E,PF⊥BC于点F.
(1)求证:AE=PE;
(2)求证:DE=DF;
(3)连接EF,EF的最小值是多少?
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】分析:(1)证明△AEP是等腰直角三角形;(2)连接CD,用SAS证明△AED≌△CFD;(3)利用CP=EF,即为求CP的最小值,当CP⊥AB时,CP取最小值.
详解:(1)∵∠C=90°,AC=BC,∴∠CAB=45°.
∵PE⊥AC,∴∠AEP=90°,∴∠APE=90°-45°=45°,
∴∠EAP=∠APE,∴AE=EP.
(2)连接CD,
∵∠C=90°,D为AB的中点,∴CD=AD.
∵AC=BC,∴∠DCF=45°,∴∠A=∠FCD,
∵PE⊥AC,PF⊥BC,∴∠CEP=∠CFP=90°,
∴四边形CEPF是矩形,∴PE=CF,∴AE=CF,
∴△AED≌△CFD(SAS),∴DE=DF.
(3)∵四边形CEPF是矩形,所以EF=CP.
∴EF最小时,CP也最小.
由垂线段最短得,当CP⊥AB时,CP最短,此时,点P与点D重合.
∵△ACP是等腰直角形,∴CP=![]() .
.
则EF的最小值是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目