Question

【题目】图1是一个八角星形纸板，图中有八个直角、八个相等的钝角，每条边都相等，如图2将纸板沿虚线进行切割，无缝隙无重叠的拼成如图3所示的大正方形，其面积为8+4 ，则图3中线段AB的长为（ ）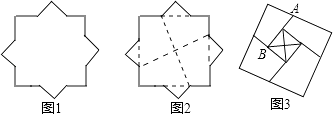
A.
B.2
C. ﹣1
D. +1

Answer 1

【答案】D
【解析】解：设八边形的边长为a， 由题意4× aa+（2a+ a）2=8+4 ，
∴a2=1，
∵a＞0，
∴a=1，
∴AB=a+ a= +1，
故选D．
【考点精析】利用正方形的性质对题目进行判断即可得到答案，需要熟知正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．