Question

【题目】在所给的11×10方格中，每个小正方形的边长都是1，按要求画出四边形，使它的四个顶点都在小正方形的顶点上．

（1）在图1中画出周长为20的菱形ABCD（非正方形）；

（2）在图2中画出邻边比为1：2，面积为40的矩形EFGH，并直接写出矩形EFGH对角线的长．

Answer 1

【答案】（1）详见解析；（2）10

【解析】

（1）根据周长为20可得菱形的边长为5，因为是非正方形，所以菱形不在格线上，由勾股定理可得两条直角边为3和4，即可画出图形；（2）根据面积为40，邻边比为1：2可得矩形的长和宽分别为4和2，以长和宽为斜边的直角三角形的直角边长分别为4、8和2、4，据此即可画图图形；根据勾股定理即可得出对角线的长.

（1）如图所示：以3、4为直角边画出斜边AB，则AB=5，同理画出其它三条边，则菱形ABCD即为所求.

（2）∵矩形EFGH的面积＝40，长：宽＝2：1，

∴长＝4，宽＝2，

∴以长和宽为斜边的直角三角形的直角边长分别为4、8和2、4，

据此即可画图图形，如图所示：

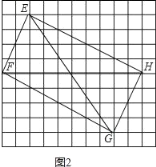
∴其对角线EG＝FH＝＝10，