题目内容
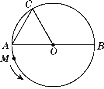
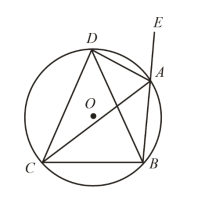
【题目】如图,AD 是△ABC 外角∠EAC 的平分线,AD 与△ABC 的外接圆⊙O 交于点 D.
(1)求证:DB=DC;
(2)若∠CAB=30°,BC=4,求劣弧 CD 的长度.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由DA平分∠EAC可得∠EAD=∠DAC,可证的∠EAD=∠DCB,∠DCB=∠DBC
可得DC=BC;
(2) 可证△COB为等边三角形,可得OC=BC=4,∠DBC=∠DCB,∠DCB=∠DBC=75°可得∠DOC的度数,可得劣弧 CD 的长度.
(1)∵DA平分∠EAC,
∴∠EAD=∠DAC
∵∠EAD+∠DAB=180°
∠DAB+∠DCB=180°
∴∠EAD=∠DCB
又∵∠DAC=∠DBC
∠DCB=∠DBC
∴DC=BC
(2)∠CDB=∠CAB=30°
∠COB=2∠CDB=60°
∴△COB为等边三角形
∴OC=BC=4
∵DC=DB
∴∠DBC=∠DCB
又∵∠DBC+∠DCB+∠CDB=180°
∴∠DCB=∠DBC=75°
∴∠DOC=2∠DBC=150°
![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目