题目内容
【题目】如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,求⊙O的半径.
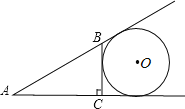
【答案】2
【解析】试题分析:分析:先连接OD、OE根据⊙O与△ABC中AB、AC的延长线及BC边相切,得出AF=AD,BE=BF,CE=CD,再根据OD⊥AD,OE⊥BC,∠ACB=90°,得出四边形ODCE是正方形,最后设OD=r,列出5+3-r=4+r,求出r=2即可.
试题解析:
连接OD、OE,
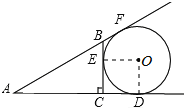
∵⊙O与△ABC中AB、AC的延长线及BC边相切,
∴AF=AD,BE=BF,CE=CD,
OD⊥AD,OE⊥BC,
∵∠ACB=90°,
∴四边形ODCE是正方形,
设OD=r,则CD=CE=r,
∵BC=3,
∴BE=BF=3-r,
∵AB=5,AC=4,
∴AF=AB+BF=5+3-r,
AD=AC+CD=4+r,
∴5+3-r=4+r,
r=2,
则⊙O的半径是2.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目