题目内容
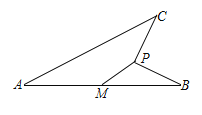
【题目】如图,线段![]() ,
,![]() 为
为![]() 的中点,动点
的中点,动点![]() 到点
到点![]() 的距离是1,连接
的距离是1,连接![]() ,线段
,线段![]() 绕点
绕点![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() ,连接
,连接![]() ,则线段
,则线段![]() 长度的最大值是( )
长度的最大值是( )
A.2B.3C.![]() D.
D.![]()
【答案】D
【解析】
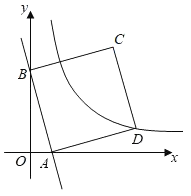
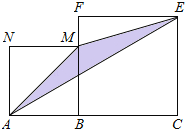
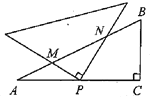
以M为坐标原点建立坐标系,过点C作CD⊥y轴,垂足为D,过点P作PE⊥DC,垂足为E,延长EP交x轴于点F,设点P的坐标为(x,y),则x2+y2=1.然后证明△ECP≌△FPB,由全等三角形的性质得到EC=PF=y,FB=EP=2x,从而得到点C(x+y,y+2x),再由勾股定理可求得AC=![]() ,最后,依据当y=1时,AC有最大值求解即可.
,最后,依据当y=1时,AC有最大值求解即可.
解:如图所示:以M为坐标原点建立坐标系,连接BC,过点C作CD⊥y轴,垂足为D,过点P作PE⊥DC,垂足为E,延长EP交x轴于点F.

∵AB=4,M为AB的中点,
∴A(2,0),B(2,0),
设点P的坐标为(x,y),则x2+y2=1,
∵∠EPC+∠BPF=90°,∠EPC+∠ECP=90°,
∴∠ECP=∠FPB,
由旋转的性质可知:PC=PB,
在△ECP和△FPB中,
 ,
,
∴△ECP≌△FPB(AAS),
∴EC=PF=y,EP=FB=2x,
∴C(x+y,y+2x),
∴AC=![]() ,
,
∵x2+y2=1,
∴AC=![]() ,
,
∵1≤y≤1,
∴当y=1时,AC有最大值,AC的最大值为![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目