题目内容
【题目】如图,在![]() 中,
中, ![]() ,将直角三角板的直角顶点与
,将直角三角板的直角顶点与![]() 边的中点
边的中点![]() 重合,直角三角板绕着点
重合,直角三角板绕着点![]() 旋转,两条直角边分别交
旋转,两条直角边分别交![]() 边于
边于![]() ,则
,则![]() 的最小值是____.
的最小值是____.
【答案】2![]()
【解析】
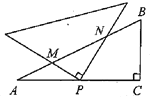
当PM=PN时,MN的值最小,过P点作PD⊥AB于点D,先证明△APD∽△ABC,再得到![]() ,再代入值,求得PD=
,再代入值,求得PD=![]() ,从而得到MN的值.
,从而得到MN的值.
∵∠C=90°,AC=10,BC=5,
∴AB=![]() ,
,
∵(PM-PN)2≥0,当PM=PN时,(PM-PN)2值最小为0,
∴MN2=PM2+PN2≥2PMPN,
当PM=PN时,PM2+PN2有最小值为2PMPN,
∴MN为最小值时,PM=PN,
过P点作PD⊥AB于点D,如图所示,
则MN=2PD,
∵∠A=∠A,∠ADP=∠ACB=90°,
∴△APD∽△ABC,
∴![]() ,即
,即![]() ,
,
∴PD=![]() ,
,
∴MN=2PD=2![]() .
.
故答案是:2![]() .
.

练习册系列答案
相关题目