题目内容
【题目】定义:对于线段![]() 和点
和点![]() ,当
,当![]() ,且
,且![]() 时,称点
时,称点![]() 为线段
为线段![]() 的“等距点”.特别地,当
的“等距点”.特别地,当![]() ,且
,且![]() 时,称点
时,称点![]() 为线段
为线段![]() 的“强等距点”.在平面直角坐标系
的“强等距点”.在平面直角坐标系![]() 中,点
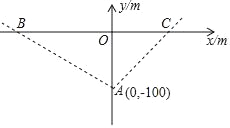
中,点![]() 的坐标为
的坐标为![]() .
.
(1)有4个点:![]() ,
,![]() ,
,![]() ,
,![]() .线段
.线段![]() 的“等距点”是 ;其中线段
的“等距点”是 ;其中线段![]() 的“强等距点”是 .
的“强等距点”是 .
(2)设第四象限有一点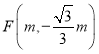 ,点
,点![]() 是线段
是线段![]() 的“强等距点”.
的“强等距点”.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②当点![]() 又为线段
又为线段![]() 的“等距点”时,求
的“等距点”时,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ,
,![]() ;
;![]() ;(2)①
;(2)① 或
或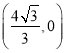 ,②
,②![]() .
.
【解析】
(1)由定义可知,线段![]() 的“等距点”在线段OA的垂直平分线上,从而得出点
的“等距点”在线段OA的垂直平分线上,从而得出点![]() ,
,![]() ,
,![]() 都在直线x=
都在直线x=![]() 上,再通过锐角三角函数判断∠OBA=120°即可解答;
上,再通过锐角三角函数判断∠OBA=120°即可解答;
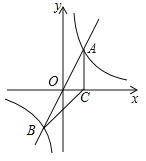
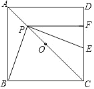
(2)①如图所示,过点F作FH⊥x轴于点H,作FK⊥y轴于点K,利用锐角三角函数得出∠HOF=∠OFK=30°,根据“强等距点”的概念得到点G在OH上或点G在KF上,再进行分类讨论,利用勾股定理表达出OG=FG即可解答;
②由(1)可知,线段OA的“等距点”都在直线x=![]() 上,过点G作GQ⊥x轴于点Q,则GQ=-t,OQ=
上,过点G作GQ⊥x轴于点Q,则GQ=-t,OQ=![]() ,根据定义以及等腰三角形的性质得到∠GOA=60°,利用tan∠GOA得到点G的坐标,结合OA∥GF即可确定m的值.
,根据定义以及等腰三角形的性质得到∠GOA=60°,利用tan∠GOA得到点G的坐标,结合OA∥GF即可确定m的值.
解:(1)由定义可知,线段![]() 的“等距点”在线段OA的垂直平分线上,
的“等距点”在线段OA的垂直平分线上,
∵点A![]() ,
,
∴线段OA的垂直平分线为直线x=![]() ,
,
如图所示,点![]() ,
,![]() ,
,![]() 都在直线x=
都在直线x=![]() 上,
上,
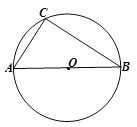
设直线x=![]() 交x轴于点Q,连接OB,AB,
交x轴于点Q,连接OB,AB,
∴OQ=![]() ,BQ=1,OB=OA,
,BQ=1,OB=OA,
∴tan∠OBQ=![]() ,
,
∴∠OBQ=60°,
∴∠OBA=2∠OBQ=120°,
∴点![]() 是线段
是线段![]() 的“强等距点”,
的“强等距点”,
连接OC,AC,OD,AD,
由图可知,∠OCA<∠OBA=120°,∠ODA<∠OBA=120°,
∴![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的“等距点”,
的“等距点”,
故答案为:B,C,D;B;
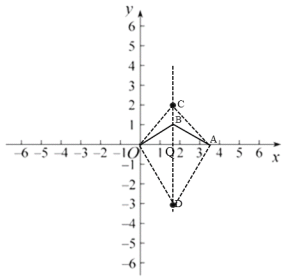
(2)①当![]() 时,
时,![]() ,
,
如图所示,过点F作FH⊥x轴于点H,作FK⊥y轴于点K,
则FH=2,OH=FK=![]() ,
,
∵tan∠HOF=![]() ,
,
∴∠HOF=30°,
∵OH∥FK,
∴∠HOF=∠OFK=30°,
∵点![]() 是线段
是线段![]() 的“强等距点”,
的“强等距点”,
∴∠OGF=120°且OG=FG,
∴∠GOF=∠GFO=30°,
∴点G在OH上或点G在KF上,
(i)当点G在OH上时,设点G(a,0)
∵OG=FG
∴![]() ,解得:
,解得:![]() ,
,
∴G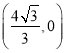 ,
,
(ii)当点G在FK上时,设点G(b,-2)
∵OG=FG
∴![]() ,解得:
,解得:![]() ,
,
∴
综上所述, 或
或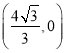
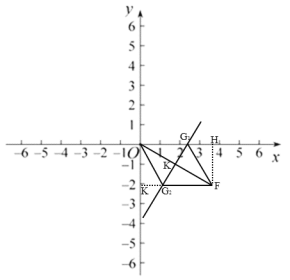
②由①可知,点G在x轴上或直线y=![]() 上,
上,
由(1)可知,线段OA的“等距点”都在直线x=![]() 上,
上,
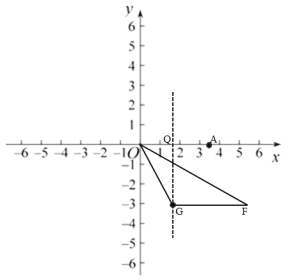
∴设点G(![]() ,t),且t≥1或t≤-1,
,t),且t≥1或t≤-1,
∴点G在第四象限,
如下图所示,过点G作GQ⊥x轴于点Q,则GQ=-t,OQ=![]() ,
,
∵点![]() 是线段
是线段![]() 的“强等距点”,
的“强等距点”,
∴∠OGF=120°,OG=FG,
∴∠OGF=∠OFG=30°,
由①可知,∠AOF=30°,
∴OA∥GF,∠GOA=60°,
∴tan∠GOA=![]() ,
,
∴t=-3,
∴![]() ,
,
解得![]() .
.

 53天天练系列答案
53天天练系列答案