ЬтФПФкШн
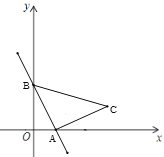
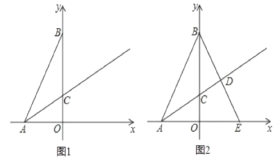
ЁОЬтФПЁПШчЭМ,ЦНУцжБНЧзјБъЯЕжа,ЕуA(6![]() ,0),ЕуB(0,18),ЁЯBAO=60ЁуЃЌЩфЯпACЦНЗжЁЯBAOНЛyжсе§АыжсгкЕуC.
,0),ЕуB(0,18),ЁЯBAO=60ЁуЃЌЩфЯпACЦНЗжЁЯBAOНЛyжсе§АыжсгкЕуC.
(1)ЧѓЕуCЕФзјБъЃЛ
(2)ЕуNДгЕуAвдУПУы2ИіЕЅЮЛЕФЫйЖШбиЯпЖЮACЯђжеЕуCдЫЖЏ,Й§ЕуNзїxжсЕФДЙЯп,ЗжБ№НЛЯпЖЮABгкЕуM,НЛЯпЖЮAOгкЕуP,ЩшЯпЖЮMPЕФГЄЖШЮЊd,ЕуPЕФдЫЖЏЪБМфЮЊt,ЧыЧѓГіdгыtЕФКЏЪ§ЙиЯЕЪН(жБНгаДГіздБфСПtЕФШЁжЕЗЖЮЇ)ЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌНЋЁїABOбиyжсЗелЃЌЕуAТфдкxжсе§АыжсЩЯЕФЕуEЃЌЯпЖЮBEНЛЩфЯпACгкЕуDЃЌЕуQЮЊЯпЖЮOBЩЯЕФЖЏЕуЃЌЕБЁїAMNгыЁїOQDШЋЕШЪБЃЌЧѓГіtжЕВЂжБНгаДГіДЫЪБЕуQЕФзјБъ.
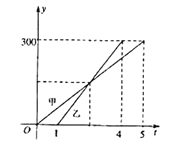
ЁОД№АИЁП(1)(0,6)ЃЛ(2 )d=3t(0<t6)ЃЛS=4t-32(t>8)ЃЛ(3) t=3,ДЫЪБQ(0,6)ЃЛt=3![]() ,ДЫЪБQ(0,18)
,ДЫЪБQ(0,18)
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШжЄУїЁЯBAO=60ЁуЃЌдкRtЁїACOжаЃЌЧѓГіOCЕФГЄМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉРэгЩД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпABЕФНтЮіЪНЃЌдйЧѓГіЕуPЕФзјБъМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉгЩЃЈ1ЃЉПЩжЊЃЌЁЯNAM=ЁЯNMA=30ЁуЃЌЭЦГіЁїAMNЪЧЕШбќШ§НЧаЮЃЌгЩЕБЁїAMNгыЁїOQDШЋЕШЃЌЁЯDOC=30ЁуЃЌЂйЕБЁЯQDO=30ЁуЪБЃЌЁїAMNгыЁїOQDШЋЕШЃЌ
ДЫЪБЕуQ![]() гыCжиКЯЃЌЕБAN=OCЪБЃЌЁїANMЁеЁїOQ
гыCжиКЯЃЌЕБAN=OCЪБЃЌЁїANMЁеЁїOQ![]() CЃЌЂкЕБЁЯOQ
CЃЌЂкЕБЁЯOQ![]() D=30ЁуЃЌЁїAMNгыЁїOQDШЋЕШЃЌДЫЪБЕуQ
D=30ЁуЃЌЁїAMNгыЁїOQDШЋЕШЃЌДЫЪБЕуQ![]() гыBжиКЯЃЌOD=AN=6
гыBжиКЯЃЌOD=AN=6![]() ЃЌЗжБ№ЧѓГіtЕФжЕМДПЩЃЛ
ЃЌЗжБ№ЧѓГіtЕФжЕМДПЩЃЛ
(1)дкRtЁїAOBжа,ЁпOA=6![]() ЃЌOB=18ЃЌ
ЃЌOB=18ЃЌ
ЁрtanЁЯBAO=![]() =
=![]() ,
,
ЁрЁЯBAO=60ЁуЃЌ
ЁпACЦНЗжЁЯBAOЃЌ
ЁрЁЯCAO=![]() ЁЯBAO=30ЁуЃЌ
ЁЯBAO=30ЁуЃЌ
ЁрOC=OAtan30Ёу=6![]()
![]() =6ЃЌ
=6ЃЌ
ЁрC(0,6).
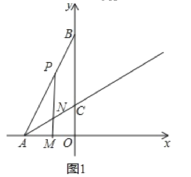
(2)ШчЭМ1жаЃЌЩшжБЯпABЕФНтЮіЪНЮЊy=kx+bЃЌ
дђга![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊy=![]() x+18ЃЌ
x+18ЃЌ
ЁпAN=2tЃЌ
ЁрAM=![]() tЃЌ
tЃЌ
ЁрOM=6![]()
![]() tЃЌ
tЃЌ
ЁрM(![]() t6
t6![]() ,0)ЃЌ
,0)ЃЌ
ЁрЕуPЕФзнзјБъЮЊy=![]() (
(![]() t6
t6![]() )+18=3tЃЌ
)+18=3tЃЌ
ЁрP(![]() t6
t6![]() ,3t)ЃЌ
,3t)ЃЌ
Ёрd=3t(0<t6).
(3)ШчЭМ2жаЃЌ
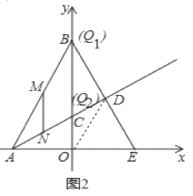
гЩ(1)ПЩжЊ,ЁЯNAM=ЁЯNMA=30ЁуЃЌ
ЁрЁїAMNЪЧЕШбќШ§НЧаЮЃЌ
ЁпЕБЁїAMNгыЁїOQDШЋЕШ,ЁЯDOC=30ЁуЃЌ
ЁрЂйЕБЁЯQDO=30ЁуЪБЃЌЁїAMNгыЁїOQDШЋЕШЃЌ
ДЫЪБЕуQ![]() гыCжиКЯ,ЕБAN=OCЪБ,ЁїANMЁеЁїOQ
гыCжиКЯ,ЕБAN=OCЪБ,ЁїANMЁеЁїOQ![]() CЃЌ
CЃЌ
Ёр2t=6ЃЌ
t=3,ДЫЪБQ(0,6).
ЂкЕБЁЯOQ![]() D=30ЁуЃЌЁїAMNгыЁїOQDШЋЕШ,ДЫЪБЕуQ
D=30ЁуЃЌЁїAMNгыЁїOQDШЋЕШ,ДЫЪБЕуQ![]() гыBжиКЯ,OD=AN=6
гыBжиКЯ,OD=AN=6![]() ЃЌ
ЃЌ
Ёр2t=6![]() ЃЌ
ЃЌ
Ёрt=3![]() ,ДЫЪБQ(0,18).
,ДЫЪБQ(0,18).

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ