题目内容
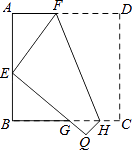
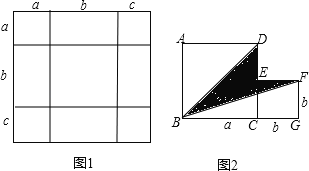
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1)，然后将剩余部分拼成一个长方形(如图2).
(1)探究：上述操作能验证的等式是 ；(请选择正确的一个)
A．a2-2ab+b2=(a-b)2 B．a2-b2=(a+b)(a-b)
C．a2+ab=a(a+b)
(2)应用：利用你从(1)选出的等式，完成下列各题：
①已知9x2-4y2=24，3x+2y=6，求3x-2y的值；
②计算：
【答案】(1)B;(2)①,4；②
【解析】
（1）根据两个图形中阴影部分的面积相等，即可列出等式；（2）①把9x2-4y2利用（1）的结论写成两个式子相乘的形式，然后把3x+2y=6代入即可求解；②利用（1）的结论化成式子相乘的形式即可求解．
（1）第一个图形中阴影部分的面积是a2-b2，第二个图形的面积是（a+b）（a-b），
则a2-b2=（a+b）（a-b）．
故答案是B；
（2）①∵9x2-4y2=（3x+2y）（3x-2y），
∴24=6（x-2y）
得：3x-2y=4；
②原式=
=
=
=
练习册系列答案
名师金手指领衔课时系列答案
相关题目
