题目内容
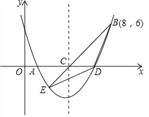
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)当![]() 为何值时反比例函数值大于一次函数的值;
为何值时反比例函数值大于一次函数的值;
(3)当![]() 为何值时一次函数值大于比例函数的值;
为何值时一次函数值大于比例函数的值;
(4)求![]() 的面积.
的面积.
【答案】(1)![]() ;
; ![]() ;(2)当
;(2)当![]() 或
或![]() 时,反比例函数值大于一次函数的值;(3)当
时,反比例函数值大于一次函数的值;(3)当![]() 或
或![]() 时,一次函数值大于比例函数的值;(4)
时,一次函数值大于比例函数的值;(4)![]() .
.
【解析】
(1)把A的坐标代入反比例函数的解析式即可求出反比例函数的解析式,把B的坐标代入求出B的坐标,把A、B的坐标代入一次函数y1=kx+b即可求出函数的解析式;
(2)根据函数的图象和A、B的坐标即可得出答案;
(3)根据函数的图象和A、B的坐标即可得出答案;
(4)求出C的坐标,求出△AOC和△BOC的面积,即可求出答案.
解:(1)∵把A(-2,1)代入![]()
得:m=-2,
∴反比例函数的解析式是y=-![]() ,
,
∵B(1,n)代入反比例函数y=-![]()
得:n=-2,
∴B的坐标是(1,-2),把A、B的坐标代入一次函数y1=kx+b得:
![]() ,
,
解得:k=-1,b=-1,
∴一次函数的解析式是y=-x-1;
(2)从图象可知:当反比例函数值大于一次函数的值时x的取值范围-2<x<0或x>1.
(3)从图象可知:当一次函数的值大于反比例函数的值时x的取值范围x<-2或0<x<1.
(4)设直线与x轴的交点为C,
∵把y=0代入一次函数的解析式是y=-x-1得:0=-x-1,
x=-1,
∴C(-1,0),
△AOB的面积S=SAOC+S△BOC=![]() ×|-1|×1+
×|-1|×1+![]() ×|-1|×|-2|=
×|-1|×|-2|=![]() .
.

【题目】某校为灾区开展了“献出我们的爱”赈灾捐款活动,九年级(1)班50名同学积极参加了这次赈灾捐款活动,因不慎,表中数据有一处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
捐款(元) | 10 | 15 | 30 | 50 | 60 | |
人数 | 3 | 6 | 11 | 11 | 13 | 6 |
(1)根据以上信息可知,被污染处的数据为 .
(2)该班捐款金额的众数为 ,中位数为 .
(3)如果用九年级(1)班捐款情况作为一个样本,请估计全校2000人中捐款在40元以上(包括40元)的人数是多少?