题目内容
【题目】甲、乙两车从![]() 城出发匀速行驶至
城出发匀速行驶至![]() 城在个行驶过程中甲乙两车离开
城在个行驶过程中甲乙两车离开![]() 城的距离
城的距离![]() (单位:千米)与甲车行驶的时间
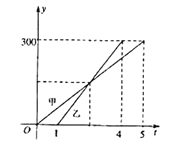
(单位:千米)与甲车行驶的时间![]() (单位:小时)之间的函数关系如图所示.则下列结论: ①
(单位:小时)之间的函数关系如图所示.则下列结论: ①![]() 两城相距
两城相距![]() 千米;②乙车比甲车晚出发
千米;②乙车比甲车晚出发![]() 小时,却早到
小时,却早到![]() 小时;③乙车出发后
小时;③乙车出发后![]() 小时追上甲车;④在乙车行驶过程中.当甲、乙两车相距
小时追上甲车;④在乙车行驶过程中.当甲、乙两车相距![]() 千米时,
千米时,![]() 或
或![]() ,其中正确的结论是_________.
,其中正确的结论是_________.
【答案】①②
【解析】
观察图象可判断①②,由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,可判断③,再令两函数解析式的差为50,可求得t,可判断④,进而得出答案.
由图象可知,A.B两城市之间的距离为300km,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,
∴①②都正确;
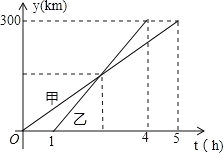
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得,k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得
![]()
解得![]()
∴y乙=100t100,
令y甲=y乙可得:60t=100t100,
解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,
∴③不正确;
令|y甲y乙|=50,可得|60t100t+100|=50,即|10040t|=50,
当10040t=50时,可解得t=![]() ,
,
当10040t=50时,可解得t=![]() ,
,
又当t=![]() 时,y甲=50,此时乙还没出发,
时,y甲=50,此时乙还没出发,
当t=![]() 时,乙到达B城,y甲=250;
时,乙到达B城,y甲=250;
综上可知当t的值为![]() 或
或![]() 或
或![]() 或t=
或t=![]() 时,两车相距50千米,
时,两车相距50千米,
∴④不正确;
综上,正确的有①②,
故答案为:①②

【题目】某校为灾区开展了“献出我们的爱”赈灾捐款活动,九年级(1)班50名同学积极参加了这次赈灾捐款活动,因不慎,表中数据有一处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
捐款(元) | 10 | 15 | 30 | 50 | 60 | |
人数 | 3 | 6 | 11 | 11 | 13 | 6 |
(1)根据以上信息可知,被污染处的数据为 .
(2)该班捐款金额的众数为 ,中位数为 .
(3)如果用九年级(1)班捐款情况作为一个样本,请估计全校2000人中捐款在40元以上(包括40元)的人数是多少?