Question

【题目】勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理，但远在毕达哥拉斯出生之前，这一定理早已被人们所利用，世界上各个文明古国都对勾股定理的发现和研究作出过贡献（希腊、中国、埃及、巴比伦、印度等），特别是定理的证明，据说有400余种方法．其中在《几何原本》中有一种证明勾股定理的方法：如图所示，作CG⊥FH，垂足为G，交AB于点P，延长FA交DE于点S，然后将正方形ACED、正方形BCNM作等面积变形，得S正方形ACED=SACQS，S正方形BCNM=SBCQT，这样就可以完成勾股定理的证明．对于该证明过程，下列结论错误的是（　　）

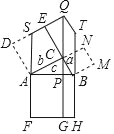
A. △ADS≌△ACB B. SACQS=S矩形APGF

C. SCBTQ=S矩形PBHG D. SE=BC

Answer 1

【答案】D

【解析】分析：根据“ASA”可证明△ADS≌△ACB，从而A正确；由△ADS≌△ACB可得AS=AB=AF，ACQS与矩形APGF等底同高，从而面积相等，故B正确；与B同理可得C正确；由S不一定是DE的中点，所以SE与BC不一定相等，故D错误.

详解：A、∵四边形ADEC是正方形，

∴AD=AC，∠DAS+∠SAC=∠SAC+∠CAB=90°，

∴∠DAS=∠BAC，

∵∠D=∠ACB=90°，

∴△ADS≌△ACB；

故A正确；

B、∵△ADS≌△ACB，

∴AS=AB=AF，

∵FS∥GQ，

∴SACQS=S矩形APGF，

故B正确；

C、同理可得：SCBTQ=S矩形PBHG；

故C正确；

D、∵△ADS≌△ACB，

∴DS=BC，

S不一定是DE的中点，所以SE与BC不一定相等，

故D错误，

本题选择结论错误的，

故选：D．