题目内容
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形![]() 是矩形
是矩形![]() 的“减半”矩形.
的“减半”矩形.
请你解决下列问题:
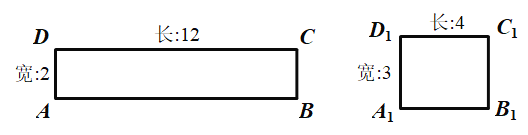
(1)当矩形的长和宽分别为![]() ,
,![]() 时,它是否存在“减半”矩形?请作出判断,并说明理由.
时,它是否存在“减半”矩形?请作出判断,并说明理由.
(2)边长为![]() 的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
【答案】(1)存在;理由见解析;(2)不存在,理由见解析.
【解析】
(1)假设存在,不妨设“减半”矩形的长和宽分别为x、y,根据如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,可列出方程组求解.
(2)正方形和其他的正方形是相似图形,周长比是2,面积比就应该是4,所以不存在“减半”正方形.
解:(1)存在
假设存在,不妨设“减半”矩形的长和宽分别为![]() ,
,![]() ,则
,则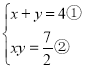 ,
,
由①,得:![]() ,③
,③
把③代入②,得![]() ,
,
解得![]() ,
,![]() .
.
所以“减半”矩形长和宽分别为![]() 与
与![]() .
.
(2)不存在
因为两个正方形是相似图形,当它们的周长比为![]() 时,面积比必定是
时,面积比必定是![]() ,
,
所以正方形不存在“减半”正方形.

练习册系列答案
相关题目