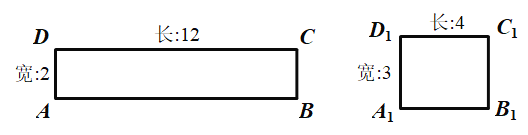
��Ŀ����
����Ŀ����ͼ����֪������y��![]() x2+
x2+![]() x��4��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
x��4��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
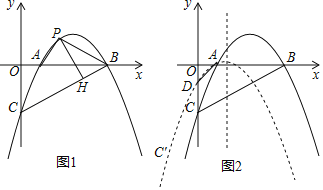
��1������BC��P���߶�BC�Ϸ��������ϵ�һ���㣬����P��PH��BC�ڵ�H����PH�������ʱ���ڡ�APB�ڲ���һ��M������AM��BM��PM����AM+![]() BM+PM����Сֵ��
BM+PM����Сֵ��
��2������D��OC���е㣬��������y��![]() x2+
x2+![]() x��4������AD����ƽ��
x��4������AD����ƽ��![]() ����λ�õ���������y�䣬C����������y������C��Ӧ�ĵ㣬������y'�ĶԳ�������һ����N����ƽ��ֱ������ϵ���Ƿ����һ��S��ʹ��C�䡢N��B��SΪ������ı����Ǿ��Σ������ڣ���ֱ��д����S�����ꣻ�������ڣ���˵�����ɣ�
����λ�õ���������y�䣬C����������y������C��Ӧ�ĵ㣬������y'�ĶԳ�������һ����N����ƽ��ֱ������ϵ���Ƿ����һ��S��ʹ��C�䡢N��B��SΪ������ı����Ǿ��Σ������ڣ���ֱ��д����S�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��AM+![]() BM+PM��
BM+PM��![]() ����2�����ڣ���S������Ϊ��S1 (
����2�����ڣ���S������Ϊ��S1 (![]() ����3+
����3+![]() )��S2 (
)��S2 (![]() ����3��
����3��![]() )��S3(
)��S3(![]() ��
��![]() )��S4(
)��S4(![]() ��
��![]() )��
)��
��������
��1������ϵ������ֱ��BC����ʽ�����P������Ϊm���ú�m�Ĵ���ʽ��ʾPQ���ٸ���PH��PQ�Ĺ�ϵ�õ�PH���ʱ��m��ֵ������PMB�Ƶ�B˳ʱ����ת120������P��M��B������MM��������P����P��R��x���ڵ�R���߶�AP����ΪAM+![]() BM+PM����Сֵ��
BM+PM����Сֵ��
��2��C����N��B��SΪ������ı����Ǿ��ο��Ը���C��B�ֱ���Ϊ���ζԽ���߷���������ۣ��ٵ�C��BΪ���ζԽ��ߣ��ڵ�C��BΪ���εıߣ�C��B��C��Nʱ���۵�C��BΪ���εıߣ�C��B��BNʱ���������N������ٸ���ƽ�ƹ�����S���꣮
��1����������y����![]() x2+
x2+![]() x��4����x��0����y����4��
x��4����x��0����y����4��
��C(0����4)��
��y��0�����![]() x2+
x2+![]() x��4��0����ã�x1��
x��4��0����ã�x1��![]() ��x2��4
��x2��4![]() ��
��
��A(![]() ��0)��B(4
��0)��B(4![]() ��0)��
��0)��
��BC��![]() ��8��
��8��
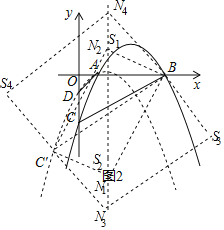
��ͼ1��

����P��PQ��x���ڵ�E��BC�ڵ�Q����PQ��y�ᣬ
���PQH����BCO��
��PH��BC��
���PHQ����BOC��90����
���PQH�ס�BCO��
��![]() ��
��![]() ��
��![]() ��
��![]() ����PH��
����PH��![]() PQ��
PQ��
��ֱ��BC����ʽΪy��kx+b����B(4![]() ��0)��C��0����4�������
��0)��C��0����4�������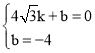 �����
�����
��ֱ��BC����ʽΪy��![]() x��4��
x��4��
��P(m��![]() +
+![]() m��4)��Q(m��
m��4)��Q(m��![]() m��4)����PQ��
m��4)����PQ��![]() +
+![]() m��
m��
��![]() ��0��0��m��4
��0��0��m��4![]() ��
��
����m��2![]() ʱ��PQ�����ֵ����ʱPH��
ʱ��PQ�����ֵ����ʱPH��![]() PQ�����ֵ��
PQ�����ֵ��
��P(2![]() ��2)��
��2)��
����PMB�Ƶ�B˳ʱ����ת120������P��M��B������MM��������P����P��R��x���ڵ�R��
��tan��PBE��![]() ��
��![]() ��
��![]() �����PBE��30����
�����PBE��30����
���P��BR��180����120����30����30����P��B��PB��4��
��P��(6![]() ��2)��AP����
��2)��AP����![]() ��
��![]() ��
��
��AM+![]() BM+PM��AM+MM��+PM��AP����
BM+PM��AM+MM��+PM��AP����![]() ��
��
��2�����ڣ���ͼ2����N(![]() ��n)��
��n)��
��D(0����2)����AD��![]() ��
��![]() ��
��
��������y����![]() x2+
x2+![]() x��4������AD����ƽ��
x��4������AD����ƽ��![]() ����λʵ��������ƽ��
����λʵ��������ƽ��![]() ����λ������ƽ��2����λ��
����λ������ƽ��2����λ��
��C��(��![]() ����6)����������y����
����6)����������y���� ��
��
����C��BΪ���ζԽ��ߣ���N��C��B�·�ʱ������ֱ��C��B����ʽΪy��![]() x��
x��![]() ��
��
�����ζԽ��߽�������Ϊ(![]() ����3)��
����3)��
��NS��C��B��![]() ��
��
��N1 (![]() ����3��
����3��![]() )��S1 (
)��S1 (![]() ����3+
����3+![]() )��
)��
N2 (![]() ����3+
����3+![]() )��S2 (
)��S2 (![]() ����3��
����3��![]() )��
)��
����C��BΪ���εıߣ�C��B��C��Nʱ����C��N2+C��B2��BN2�ɵã�
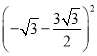 +(��6��n)2+
+(��6��n)2+![]() +(��6��0)2
+(��6��0)2
��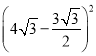 +(0��n)2��
+(0��n)2��
��ã�n����![]() ��N3(
��N3(![]() ����
����![]() )��
)��
��C��N��BS��
��S3(![]() ��
��![]() )��
)��
����C��BΪ���εıߣ�C��B��BNʱ����BN2+C��B2��C��N2�ɵã�
 +(n��0)2+
+(n��0)2+![]() +(��6��0)2
+(��6��0)2
��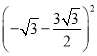 +(��6��n)2��
+(��6��n)2��
��ã�n��![]()
��N4(![]() ��
��![]() )��
)��
��BN��C��S��
��S4(![]() ��
��![]() )��
)��
������������S��������S1 (![]() ����3+
����3+![]() )��S2 (
)��S2 (![]() ����3��
����3��![]() )��S3(
)��S3(![]() ��
��![]() )��S4(
)��S4(![]() ��
��![]() )��
)��

����Ŀ������һ�и�У�����п�����ѧ�ƿ�����������ѮԲ���������ڳ��ڱ�ս�忼�Ĺ����У�ѧ������������Ҳ����Ȼ�����仯��ij���ܲ��Ի�������У����ѧ�������������еijɼ�ת���ɵ������ͱ�������ָ�꣨�ٷ��ƣ���Ϊ���ܲ��Գɼ������������ݷ����о���ν�һ�����ѧ�����������ʣ�
�����ռ��û����ƻ�ѡȡ100��ѧ�������ܲ��Գɼ���Ϊ�������ṩ���������ֳ������鷽����
A����ȡ�����꼶�ʹ�У����100��ѧ�������ܲ��Գɼ��������
B����ȡȫ�꼶�����ɼ��Ϻõ�ѧ����100��ѧ�������ܲ��Գɼ��������
C����ȫ�꼶�����ѡȡ�С�Ů��50��ѧ�������ܲ��Գɼ��������
��������������
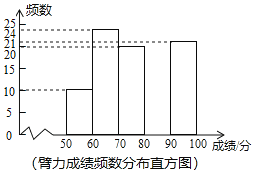
a�����ݷֳ�5�飺90��x��100��80��x��90��70��x��80��60��x��70��50��x��60������90������Ϊ���㣮�������ɼ�ͳ�Ʊ��ͱ����ɼ�Ƶ���ֲ�ֱ��ͼ���£�
�������ɼ� | ���� | ���� |
90��x��100 | p | |
80��x��90 | �������������B | 37 |
70��x��80 | ���������� | 23 |
60��x��70 | ��һ | 6 |
50��x��60 | �� | 5 |
�ϼ� | 100 | 100 |
���������ɼ�ͳ�Ʊ���
b�������ɼ���70��x��80��һ��ľ���������£�
70 71 71 71.5 72 73 73.5 74 74 74
74.5 74.5 75 75.5 75.5 76 76 77 78 79
c���������ͱ�������ָ��ɼ���ƽ��������λ����������������ͳ�����£�
����ָ�� | ƽ�������֣� | ��λ�����֣� | �������֣� | ������ |
������ | 82.5 | 89 | 83 | m |
���� | 77 | n | 81 | 21% |
���ݷ�������������Ϣ���ش��������⣺
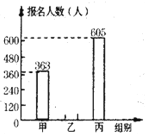
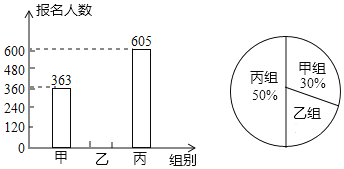
��1���������ֳ��������У�����Ϊ����������� ��������ĸ����
��2����ȫ�����ɼ�Ƶ���ֲ�ֱ��ͼ�����������ݵã�m���� ����n���� ����
��3���ڴ˴β����У�ijѧ���ĵ������ɼ�Ϊ87�֣������ɼ�Ϊ78�֣�����ѧ���ɼ���������ǰ��ָ������ ������������������������������� ����
����Ŀ��ѧУ��ѧ���ŵ�ͬѧ����ѧ���п�չ���˽�Уѵ�������ĵ�������ȡ��������ķ�ʽ�����ʾ����飮�ʾ�����Ľ����Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ���࣮
���࣮![]() ���ʾ�dz��˽⣻
���ʾ�dz��˽⣻![]() ���ʾ�Ƚ��˽⣻
���ʾ�Ƚ��˽⣻![]() ���ʾ�����˽⣻
���ʾ�����˽⣻![]() ���ʾ��̫�˽⣮��Ҫ��ÿλͬѧ����ѡ����ֻ��ѡ��һ�ͳ���������������
���ʾ��̫�˽⣮��Ҫ��ÿλͬѧ����ѡ����ֻ��ѡ��һ�ͳ���������������
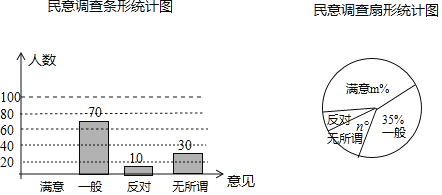
��� | Ƶ�� | Ƶ�� |
| 20 |
|
|
| 0.3 |
| 11 | 0.22 |
| 4 | 0.08 |
��1������![]() __________��
__________��![]()
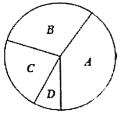
��2�����ݱ������ݣ����![]() ��ͬѧ������Ӧ������Բ�Ľ�Ϊ_________�ȣ�
��ͬѧ������Ӧ������Բ�Ľ�Ϊ_________�ȣ�
��3�����ݵ�������������Ƹ�У1500��ѧ���ж�Уѵ���dz��˽�����������
��4��ѧУ�ڿ�չ�˽�Уѵ�����У���Ҫ��![]() ��ļס��ҡ�����������ͬѧ�����ѡȡ2�˲μ�չʾ�����ǡ��ѡ�м������˵ĸ��ʣ��������б���������״ͼ��ʾ��
��ļס��ҡ�����������ͬѧ�����ѡȡ2�˲μ�չʾ�����ǡ��ѡ�м������˵ĸ��ʣ��������б���������״ͼ��ʾ��