Question

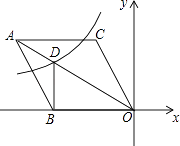
【题目】（1）在平面直角坐标系中，OABC的边OC落在x轴的正半轴上，且点C（4，0），B（6，2），直线y=2x+b将OABC的面积平分，则b=_______.

（2）在平面直角坐标系中，直线y＝2x＋3关于原点对称的直线的表达式为__________．

Answer 1

【答案】-5； y＝2x－3.

【解析】

（1）先确定OABC对角线交点坐标，再代入y=2x+b中，即可求出b的值；

（2）根据两条直线关于原点对称，则这两条直线平行，即k的值不变． 与y轴的交点关于原点对称，即b的值互为相反数，即可得出答案.

解：（1）在OABC中，

∵边OC落在x轴的正半轴上，且点C（4，0），B（6，2），

∴对角线交点的坐标，即线段OB的中心坐标为（3，1），

∵直线y=2x+b将OABC的面积平分，

∴直线y=2x+b过点（3，1），

把（3，1）代入y=2x+b得，

，

解得，b=-5，

故答案为：-5；

（2）设与直线y＝2x＋3关于原点对称的直线的解析式为y=kx+b，

∵这两条直线关于原点对称，

∴这两条直线平行，即k=2，

∵这两条直线与y轴的交点关于原点对称，

∴b=-3，

∴y＝2x－3.

故答案为：y＝2x－3.