ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΘΚΦΉΓΔ““ΝΫ≥ΒΖ÷±π¥”œύΨύ300«ßΟΉΒΡ A,BΝΫΒΊΆ§ ±≥ωΖΔœύœρΕχ––Θ§Τδ÷–ΦΉΒΫ BΒΊΚσΝΔΦ¥ΖΒΜΊΘ§œ¬ΆΦ «ΥϋΟ«άκΗςΉ‘≥ωΖΔΒΊΒΡΨύάκyΘ®«ßΟΉΘ©”κ–– Μ ±ΦδxΘ®–Γ ±Θ©÷°ΦδΒΡΚ· ΐΆΦœσΘ°
Θ®1Θ©«σΦΉ≥Βάκ≥ωΖΔΒΊΒΡΨύάκ yΘ®«ßΟΉΘ©”κ–– Μ ±ΦδxΘ®–Γ ±Θ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωΉ‘±δΝΩΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©Β±ΥϋΟ«–– ΜΒΫ”κΗςΉ‘≥ωΖΔΒΊΒΡΨύάκœύΒ» ±Θ§”ΟΝΥ ![]() –Γ ±Θ§«σ““≥Βάκ≥ωΖΔΒΊΒΡΨύάκ yΘ®«ßΟΉΘ©”κ–– Μ ±Φδ xΘ®–Γ ±Θ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
–Γ ±Θ§«σ““≥Βάκ≥ωΖΔΒΊΒΡΨύάκ yΘ®«ßΟΉΘ©”κ–– Μ ±Φδ xΘ®–Γ ±Θ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§«σΥϋΟ«‘Ύ–– ΜΒΡΙΐ≥Χ÷–œύ”ωΒΡ ±ΦδΘ°
ΓΨ¥πΑΗΓΩΦϊΫβΈω
ΓΨΫβΈωΓΩΖ÷ΈωΘΚ
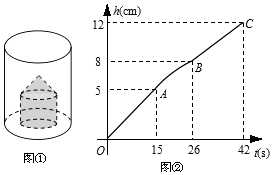
Θ®1Θ©”…ΆΦ÷ΣΘ§ΗΟΚ· ΐΙΊœΒ‘Ύ≤ΜΆ§ΒΡ ±Φδάο±μœ÷≥…≤ΜΆ§ΒΡΙΊœΒΘ§–ηΖ÷ΕΈ±μ¥οΘ°Β±–– Μ ±Φδ–Γ”Ύ3 ± «’ΐ±»άΐΚ· ΐΘΜΒ±–– Ι ±Φδ¥σ”Ύ3–Γ”Ύ![]() ± «“Μ¥ΈΚ· ΐΘ°Ω…ΗυΨί¥ΐΕ®œΒ ΐΖ®Ν–ΖΫ≥ΧΘ§«σΚ· ΐΙΊœΒ ΫΘ°
± «“Μ¥ΈΚ· ΐΘ°Ω…ΗυΨί¥ΐΕ®œΒ ΐΖ®Ν–ΖΫ≥ΧΘ§«σΚ· ΐΙΊœΒ ΫΘ°
Θ®2Θ©4.5–Γ ±¥σ”Ύ3Θ§¥ζ»κ“Μ¥ΈΚ· ΐΙΊœΒ ΫΘ§ΦΤΥψ≥ω““≥Β‘Ύ”ΟΝΥ![]() –Γ ±–– ΙΒΡΨύάκΘ°¥”ΆΦœσΩ…Ω¥≥ω«σ““≥Βάκ≥ωΖΔΒΊΒΡΨύάκyΘ®«ßΟΉΘ©”κ–– Μ ±ΦδxΘ®–Γ ±Θ©÷°Φδ «’ΐ±»άΐΚ· ΐΙΊœΒΘ§”Ο¥ΐΕ®œΒ ΐΖ®Ω…«σΫβΘ°
–Γ ±–– ΙΒΡΨύάκΘ°¥”ΆΦœσΩ…Ω¥≥ω«σ““≥Βάκ≥ωΖΔΒΊΒΡΨύάκyΘ®«ßΟΉΘ©”κ–– Μ ±ΦδxΘ®–Γ ±Θ©÷°Φδ «’ΐ±»άΐΚ· ΐΙΊœΒΘ§”Ο¥ΐΕ®œΒ ΐΖ®Ω…«σΫβΘ°
Θ®3Θ©ΝΫ’ΏœύœρΕχ––Θ§œύ”ω ±ΦΉΓΔ““ΝΫ≥Β–– ΙΒΡΨύάκ÷°ΚΆΈΣ300«ßΟΉΘ§Ν–≥ωΖΫ≥ΧΫβ¥πΘ§”…Χβ“β”–ΝΫ¥Έœύ”ωΘ°
œξΫβΘΚ
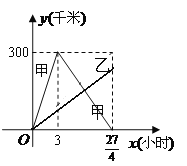
Θ®1Θ©Θ®1Θ©Β±0ΓήxΓή3 ±Θ§ «’ΐ±»άΐΚ· ΐΘ§…ηΈΣy=kxΘ§
x=3 ±Θ§y=300Θ§¥ζ»κΫβΒΟk=100Θ§Υυ“‘y=100xΘΜ
Β±3ΘΦxΓή![]() ±Θ§ «“Μ¥ΈΚ· ΐΘ§…ηΈΣy=kx+bΘ§
±Θ§ «“Μ¥ΈΚ· ΐΘ§…ηΈΣy=kx+bΘ§
¥ζ»κΝΫΒψΘ®3Θ§300Θ©ΓΔΘ®![]() Θ§0Θ©Θ§ΒΟ
Θ§0Θ©Θ§ΒΟ
ΫβΒΟ![]() Θ§
Θ§
Υυ“‘y=540©¹80xΘ°
ΉέΚœ“‘…œΒΟΦΉ≥Βάκ≥ωΖΔΒΊΒΡΨύάκy”κ–– Μ ±Φδx÷°ΦδΒΡΚ· ΐΙΊœΒ Ϋ ΈΣΘΚy= Θ°
Θ°
Θ®2Θ©Β±x=![]() ±Θ§yΦΉ=540©¹80ΓΝ
±Θ§yΦΉ=540©¹80ΓΝ![]() =180ΘΜ
=180ΘΜ
““≥ΒΙΐΒψΘ®![]() Θ§180Θ©Θ§y““=40xΘ°Θ®0ΓήxΓή
Θ§180Θ©Θ§y““=40xΘ°Θ®0ΓήxΓή![]() Θ©
Θ©
Θ®3Θ©”…Χβ“β”–ΝΫ¥Έœύ”ωΘ°
ΔΌΒ±0ΓήxΓή3Θ§100x+40x=300Θ§ΫβΒΟx=![]() ΘΜ
ΘΜ
ΔΎΒ±3ΘΦxΓή![]() ±Θ§Θ®540©¹80xΘ©+40x=300Θ§ΫβΒΟx=6Θ°
±Θ§Θ®540©¹80xΘ©+40x=300Θ§ΫβΒΟx=6Θ°
Ήέ…œΥυ ωΘ§ΝΫ≥ΒΒΎ“Μ¥Έœύ”ω ±ΦδΈΣΒΎ![]() –Γ ±Θ§ΒΎΕΰ¥Έœύ”ω ±ΦδΈΣΒΎ6–Γ ±Θ°
–Γ ±Θ§ΒΎΕΰ¥Έœύ”ω ±ΦδΈΣΒΎ6–Γ ±Θ°

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ‘ΡΕΝΕ‘»Υ≥…≥ΛΒΡ”Αœλ «Ψό¥σΒΡΘ§“Μ±ΨΚΟ ιΆυΆυΡήΗΡ±δ»ΥΒΡ“Μ…ζΘ§ΟΩΡξΒΡ4‘¬23»’±ΜΝΣΚœΙζΫΧΩΤΈΡΉι÷·»ΖΕ®ΈΣΓΑ άΫγΕΝ ι»’Γ±Ρ≥–Θ±Ψ―ßΡξΩΣ’ΙΝΥΕΝ ιΜνΕ·Θ§‘Ύ’β¥ΈΜνΕ·÷–Θ§ΑΥΡξΦΕ![]() Αύ40Οϊ―ß…ζΕΝ ι≤α ΐΒΡ«ιΩω»γ±μ
Αύ40Οϊ―ß…ζΕΝ ι≤α ΐΒΡ«ιΩω»γ±μ
ΕΝ ι≤α ΐ | 4 | 5 | 6 | 7 | 8 |
»Υ ΐ | 6 | 4 | 10 | 12 | 8 |
ΗυΨί±μ÷–ΒΡ ΐΨίΘ§«σΘΚ
(1)ΗΟΑύ―ß…ζΕΝ ι≤α ΐΒΡΤΫΨυ ΐΘΜ
(2)ΗΟΑύ―ß…ζΕΝ ι≤α ΐΒΡ÷–ΈΜ ΐΘ°